zbadaj ciągłość piotrek:

	x
{		dla x mniejszego od 0 i x≠− 3
	x2−9

f(x) {

	x
{		} dla x≥0 i x= −3
	x2+1

piotrek: prosze o pomoc

piotrek: potrzebuje rozwiązanie tego zadania

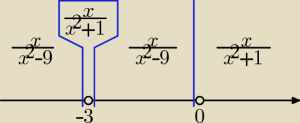Bogdan: Badamy ciągłość w punkcie x = −3.

	−3		−3
f(−3) =		=
	9 + 1		10

	x		−3		−3
lim(x→−3−)		=		= −∞ ≠
	(x − 3)(x + 3)		−6 * 0−		10

Funkcja f(x) w punkcie x = −3 nie jest ciągła. Badamy ciągłość w punkcie x = 0.

	0
f(0) =		= 0
	02 + 1

	x
lim(x→−0−)		= 0
	x2 − 9

	x
lim(x→−0+)		= 0
	x2 + 1

lim_(x→0) f(x) = f(0) Funkcja w punkcie x = 0 jest ciągła.

piotrek: wielkie dzięki prosze jeszcze o sprawdzenie jednego zadania

	x+3
{		dla x≠−3 i x≠2
	x2+x−6

f(x) {

	1
{ −		dla x=−3 i x=2
	5

badam ciagłośc w pkt −3 f(−3)=0

	1		1
lim x→−3− =		= −
	x−2		5

	1
lim x→−3+ = −
	5

badam ciągłość w pkt 2 f(2)= ∞

	1
limx→2−=−
	5

	1
limx→2+= −
	5

Bogdan:

	1
f(−3) = −		, w punkcie −3 funkcja jest ciągła.
	5

	1
f(2) = −		, wyznacz granice f(x) przy x→2− oraz x→2+
	5

piotrek:

	1
mogłbys mi wyjaśnić dlaczego f(−3)= −		? bo mi wychodzi 0
	5

	1
a także f(2)=−		?
	5

	1		1
limx→2−i+= −		bo dla x=2 funkcja wynosi −		tak?
	5		5