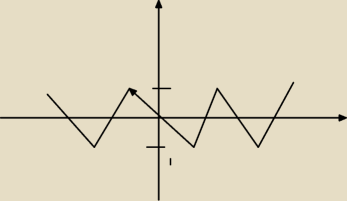
funkcja czekolada: rysunek przedstawia fragment wykresu funkcji y=f(x) otrzymanego z wykresu funkcji g(x)=sinx w wyniku odpowiednich przeklsztalcen . najdz wzor funkcji f i rowiaz rownanie f(x)=−√3 poniewaz nie wiem jak tutaj sie rysuje, wiec: tam min i max funkcji to 2 i −2. a prechodzi na osi 'x' przez punkty : −π, −π/2 , 0, π/2 , π , 3/2π

sushi_ gg6397228: funkcja jest rozciagnieta do gory i dołu f₁= 2* sin x

	π
okres miejsc zerowych jest co		−−> normalnie jest co π
	2

f₂= 2* sin 2x funkcja jest odbita symetrycznie wzgledem osi OX f₃= −2* sin 2x

czekolada: a wlasnie chyba nie jest odbita.. mi wyszlo ze 2sin2x ... ale jak to teraz rozwiazac dla −√3 ?

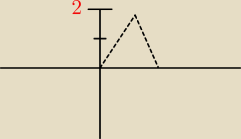
sushi_ gg6397228: tak wyglada poczatek sinusa dla pierwszej cwiartki, wiec Twoja 2 sin 2x jest dla takiego rysunku

sushi_ gg6397228: −2 sin 2x= −√3

	√3
sin 2x=
	2

rysunek normalnego sinusa i odczytanie "dwoch wartosci + 2 k π" a potem podzielenie przez "2" co stoi przy argumencie

czekolada: dziekujee ; )