zadanie z parameterm prosze o pomoc Hubb: wyznacz te wartości parametru m dla których każdy z dwóch różnych pierwiastków równania x² − 6mx + 2 − 2m + 9m² = 0 jest większy od 3 błagam o pomoc nie mam pojęcia jak to zrobic wiem tylko że żeby były dwa miejsca zerowe delta musi być większa od zera

magda: najpierw uporządkować x²−6mx+(2−2m+9m²)=0 jest to równanie kwadratowe a=1 b=−6m c=2−2m+9m² wylicz deltę Δ=b²−4ac skoro mają być dwa pierwiastki zatem Δ>0

nikka: ale musi być jeszcze warunek na to, żeby pierwiastki były większe od 3 ...

Januszek75: plus warunek z Viete'a, że x1 * x2 > 9 x1 + X2 > 6

Tragos: { Δ > 0 { x₁ > 3 { x₂ > 3 { Δ > 0 { x₁ − 3 > 0 { x₂ − 3 > 0 { Δ > 0 { (x₁ − 3)(x₂ − 3) > 0 { x₁ − 3 + x₂ − 3 > 0 { Δ > 0 { x₁*x₂ − 3x₁ − 3x₂ + 9 > 0 { x₁ + x₂ − 6 > 0 { Δ > 0 { x1*x₂ − 3(x₁ + x₂) + 9 > 0 { x₁ + x₂ − 6 > 0 teraz wystarczy zastosować wzory Viete'a, rozwiązać i gotowe

Hubb: nie wiem czy dobrze wylicyłem delte wyszło mi Δ= 36m² − 4 (2 − 2m + 9m²) = 36m² − 8 + 8m −36m² = 8m − m Δ > 0 ⇔ m>1 dobrze to jest

Hubb: wielkie dzieki za rozwiazanie ale ja nie mam pojecia z kad to wychodzi

Tragos: dwa różne pierwiastki, stąd Δ > 0 każdy z nich ma być większy od 3, czyli: x₁ > 3 x₂ > 3 x₁ − 3 > 0 x₂ − 3 > 0 aby (x₁ − 3) i (x₂ i 3) było > 0 to ich iloczyn musi być większy od 0 i ich suma większa od zero, potem trzeba tak umiejętnie wyciągnąć przed nawias, by móc zastosować wzory Viete'a −−−−−−−− Δ = 36m² − 4(2 − 2m + 9m²) = 36m² − 8 + 8m − 36m² = 8m − 8 Δ > 0 8m − 8 > 0 8m > 8 m > 1

Hubb: dzieeki dzieki chyba juz wiem

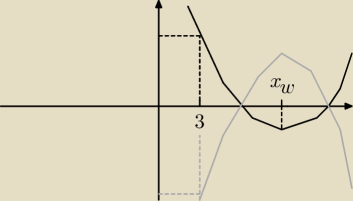
Godzio: Właściwie to powinno być tak zrobione: Δ > 0 a > 0 x_w > 0 f(3) > 0 lub Δ > 0 a < 0 x_w > 0 f(3) < 0

Eta:

Hubb:

Hubb: w zbiorze mam nawet przykład ale nic on mi nie mówi

Godzio: a sorki, tam gdzie a < 0 możesz wywalić bo wydawało mi się ze widziałem mx² + ...

Godzio: To jest zadanie w którym nie trzeba korzystać z viete'a, wystarczy narysować wykres który spełnia wymogi zadania i zobaczyć jakie warunki musi spełniać żeby było to prawdziwe dla jakieś parametru

Hubb: Δ > 0 a > 0 xw > 0 f(3) > 0 Δ = 36m2 − 4(2 − 2m + 9m2) = 36m2 − 8 + 8m − 36m2 = 8m − 8 Δ > 0 8m − 8 > 0 8m > 8 m > 1 co dalej?

Hubb: w tym przykładzie który mam podany nie ma wzorów vieta

Godzio: x² − 6mx + 2 − 2m + 9m² = 0 Δ = 36m² − 8 + 8m − 36m² > 0 ⇒ 8m > 8 ⇒ m > 1

	−b		6m
xw =		=		= −3m > 0 ⇔ m > 0
	2a		2

	11
f(3) > 0 ⇒ 9 − 18m + 2 − 2m + 9m2 > 0 ⇒ 9m2 − 20m + 11 > 0 ⇒ m ∊ (−∞,1) ∪(		,∞)
	9

Rozwiązaniem jest część wspólna wszystkich rozwiązań, teraz podaj odpowiedź

Godzio: literówka: ... = 3m > 0 => m > 0

Hubb: dziękuję bardzo!

Hubb: m ∊ (11/9 ∞)

Hubb: wreszcie ktoś mi pomógł

Godzio: ok

Nat: Jejku a dlaczego xw musi być większe od 0?

Inka : Nie musi byc >0 Ono jest >0 z tresci zadania .masz x² wiec a=1>0