| 5 | ||
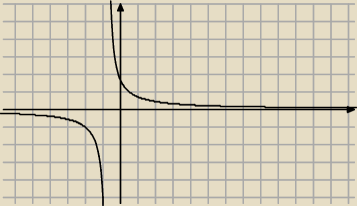
f(x)= | ||
| 3+4x |
| 3 | ||
x≠− | ||
| 4 |
| 3 | ||
⋀x1,x2∊ℛ\{− | } x1≠x2 ⇒f(x1)≠f(x2) | |
| 4 |
| 5 | ||
f(x1)= | ||
| 3+4x1 |
| 5 | ||
f(x2)= | ||
| 3+4x2 |
| 5 | 5 | ||
− | ≠0 | ||
| 3+4x1 | 3+4x2 |
| 5(3+4x1) | ||
U{5(3+4x2)− | ≠0 | |
| (3+4x1)(3+4x2) |
| 15−20x2−15+20x1 | |
≠0 | |
| (3+4x1)(3+4x2) |
| −20x2+20x1 | |
≠0 | |
| (3+4x1)(3+4x2) |
| 20x1−20x2 | |
≠0 | |
| (3+4x1)(3+4x2) |
| 3 | ||
(3+4x1)(3+4x2)≠0 gdyz x1≠x2≠− | więc żaden z dwóch czynników nie będzie równy zero | |
| 4 |
| 5 | ||
Wniosek. Funkcja f(x)= | w swojej naturalnej dziedzinie jest różnowartościowa | |
| 3+4x |