rozwiaz nierownosc z wartoscia bezwzgledna gosiaa: |x−2|+|6−2x|+x<0

adrian: Najpierw szukamy miejsc dla których wartości bezwzględne wyniosą 0, czyli: x−2=0 x=2 6−2x=0 2x=6 x=3 x=0 No to mamy 3 przedziały teraz: 1. (−∞;0) 2.<0;2) 3. <2;3) 4. <3:+∞) I teraz po kolei badasz przedziały, czyli jeżeli wartosc pod wartością bezwględną jest ujemna dla kazdego argumentu z tego przedziału to zdejmujesz wartosc bezwzgledną ale ze zmianą znaku: Następnie rozwiązujesz nierówność. Kolejny krok to porównanie Twojego rozwiązania z każdego przedziału z owym przedziałem, czyli wybiersz część wspólną tego co, Ci wyszło i danego przedziału. Na koniec jak juz masz wszystkie rozwiązania ustalone, zestawiasz je, sumując.

adrian: 4 przedziały oczywiscie

adrian: Poprawka,bez tego x=0: 3 przedziały: 1. (−∞;2) 2. <2;3) 3. <3:+∞)

zosiaa: kurcze...tego "I teraz po kolei badasz przedziały, czyli jeżeli wartosc pod wartością bezwględną jest ujemna dla kazdego argumentu z tego przedziału to zdejmujesz wartosc bezwzgledną ale ze zmianą znaku: Następnie rozwiązujesz nierówność. Kolejny krok to porównanie Twojego rozwiązania z każdego przedziału z owym przedziałem, czyli wybiersz część wspólną tego co, Ci wyszło i danego przedziału. Na koniec jak juz masz wszystkie rozwiązania ustalone, zestawiasz je, sumując." to ja juz za bardzo nie rozumiem... moglbys mi pokazac na 1 przykladzie chcociaz?a ja jak zoabcze to juz reszte zrobie

adrian: Proszę: 1. (−∞;2) |x−2|+|6−2x|+x<0 Uproścmy sobie: |x−2|+2|3−x|+x<0 Tutaj widzimy, że nasza 1 wartośc bezwzględna jest ujemna dla każdego X, z tego przedziału, wiec zdejmujemy wartość ale ze zmianą znaku.Druga zaś, jest zawsze dodatni, wiec zdjemujemy wartosc bezwzgledna ale bez zmiany znaku −x+2+6−2x+x<0 −2x+8 < 0 −x+4 < 0 x > 4 Bierzemy czesc wspolna z przedzialem (−∞;2) Czyli x∊ [] zbiór pusty.Zaden X tutaj nam sie nie zgra z nierownoscia.

magda: ok super.dzieki!

Ula: |x−2|<15 jak to rozwiązać?:(

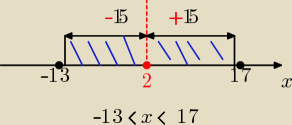
Eta: 1 sposób .... z interpretacji geometrycznej modułu ( rys) x€ ( −13, 17) 2 sposób −15< x −2 <15 / +2 −13 < x < 17 => x€( −13, 17) 3 sposób | x−2| <15 => x−2 < 15 i x−2 > −15 x < 17 i x > −13 x€ ( −13, 17)

jam nie zdam :): |x+3|≤0 ?