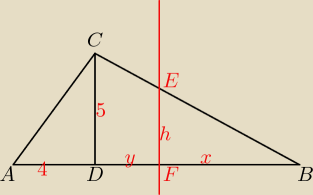
 wysokosc CD trojkata, ktorej dlugosc wynosi 5 cm, dzieli bok AB na dwa odcinki tak, że:
|AD|=4cm i |DB|=8cm
w tym trojkacie poprowadzono prostą EF rownoległą do CD, ktora podzieliła ten trójkąt na dwie
figury o równych polach tak, że E∊BC i F∊AB.
oblicz dlugosc odcinka leżącego na tej prostej, zawartego w tym trojkacie.
mogłby ktoś to zadanie zrobić i wytlumaczyć w przystepny sposób?
wysokosc CD trojkata, ktorej dlugosc wynosi 5 cm, dzieli bok AB na dwa odcinki tak, że:
|AD|=4cm i |DB|=8cm
w tym trojkacie poprowadzono prostą EF rownoległą do CD, ktora podzieliła ten trójkąt na dwie
figury o równych polach tak, że E∊BC i F∊AB.
oblicz dlugosc odcinka leżącego na tej prostej, zawartego w tym trojkacie.
mogłby ktoś to zadanie zrobić i wytlumaczyć w przystepny sposób?
 naprawdę nie wiem jak mam się do tego zabrać
naprawdę nie wiem jak mam się do tego zabrać
 x+y=8
tr.BFE ~ tr.BDC
x+y=8
tr.BFE ~ tr.BDC
| x | h | ||
= | |||
| x+y | 5 |
| x | h | ||
= | |||
| 8 | 5 |
| 8h | ||
x= | ||
| 5 |
| x*h | 85h2 | 4h2 | ||||
P1= | = | = | ||||
| 2 | 2 | 5 |
| 4*5 | h+5 | |||
P2= | + | *y = | ||
| 2 | 2 |
| h+5 | ||
10+ | *(8−x) = | |
| 2 |
| h+5 | ||
10+ | *(8−8h5) = | |
| 2 |
| h+5 | ||
10+ | *(40−8h5)= | |
| 2 |
| (h+5)*8(5−h) | ||
10+ | = | |
| 10 |
| 100+8(5h−h2+25−5h) | |
= | |
| 10 |
| −8h2+200+100 | |
= | |
| 10 |
| −2(4h2−150) | |
= | |
| 10 |
| −4h2+150 | |
| 5 |
| 4h2 | −4h2+150 | ||
= | /*5 | ||
| 5 | 5 |
| √75 | 5√3 | |||
h = | = | |||
| 2 | 2 |