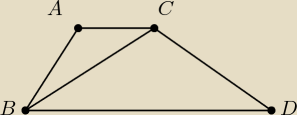
Kąty w trapezie Mexx: Ma wyglądać mniej więcej tak ( gdyby było coś niejasnego ) Mam znaleźć kąty w trapezie, który : a) ma 1. ramię równe podstawie b) przekątną ( Lewy Dół [ LD ] − Prawa Góra [ PG ] ) równą 2. ramieniu c) podstawę równą sumie obu ramion Jednym słowem pomocy

Mexx: Odświeżam

Mexx: Odświeżam

Mexx: Odświeżam

Mexx: Odświeżam

Basia: jeżeli dobrze rozumiem (a nie jestem pewna) AB = AC BC=2=CD BD=AB+CD sprawdź czy o to chodzi

Mexx: Dokładnie , tylko nie rozumiem tej 2 pomiędzy BC=CD Z góry dzięki

Basia: to chochlik, nie ma jej tam być

Basia: rozwiązałam, ale cierpliwości muszę to narysować

Mexx: Odświeżam Zależy mi na czasie , mam to na jutro do szkoły , zadanie dodatkowe na 5

krzyś: ja ci nie pomogę, przerasta mnie a też mam podobne

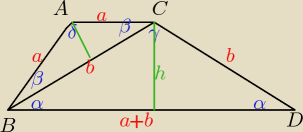
Basia: γ=180−2α δ=180−2β δ=180−(α+β) 180−2β=180−α−β α=β i γ=δ tr.BAC i tr.BCD są podobne równoramienne skala podobieństwa s=^a_b a=s*b a+b = sb+b=b(s+1)

	a+b2		b(s+1)2		s+1
cosα=		=		=
	b		b		2

	b2		b		b		1
cosα=		=		=		=
	a		2a		2sb		2s

s+1		1
	=
2		2s

s+1=¹_s s²+s=1 s²+s−1=0 Δ=1+4=5

	−1−√5
s1=		niemożliwe
	2

	−1+√5
s2=
	2

	−1+√5
s=
	2

	1		1+√5
cosα=		=
	√5−1		4

mając cosα mogę policzyć sinα (∡D) potem sin2α i cos2α (∡B) sin(180−α) i cos(180−α) czyli (∡C) sin(180−2α) i cos(180−2α) czyli (∡A) co jest równoznaczne z policzeniem tych kątów nie wiem czy się gdzieś w rachunkach nie pomyliłam szukam czegoś prostszego, ale na razie nie widzę

Mexx: ło jezuu ... my się jeszcze nie uczyliśmy sinusów itp. , nie dziwię się że nie mogłem rozwiązać , dzięki

Basia: a jaka to szkoła ? gimnazjum ? bo jeżeli gimnazjum to musi być prostszy sposób

krzyś: to nie jest poziom 1 gimnazjum

krzyś: ale jaki ?

Mexx: może kąty przyległe , jakieś właściwości po podzieleniu tr. przez wysokość ?

Basia: Mexx napisz do jakiej szkoły chodzisz

Mexx: Musi mieć coś z wysokości i tr. równoramiennymi , bo rozwiązanie trzeba podać w stopniach

Mexx: 1 kl. Gimn. − coś więcej ?

Basia: proste jak budowa cepa; zaraz to napiszę

Basia: w tych obliczeniach musiałam się pomylić, rysuję jeszcze raz moment

Basia: CE || AB ⇒ BE=a i CE=a ⇒ DE=b ∡BAC = 180−2β ∡BAC = 180−(α+β) 180−2β=180−α−β α=β ∡DCB = 180−2α ∡DCB = α+γ 180−2α=α+γ 3α=180−γ γ=180−3α

	180−α
γ=
	2

	180−α
180−3α=		/*2
	2

360−6α=180−α 5α=180 α=36 reszta to pikuś (może się i nie pomyliłam cos36 może tyle wynosić)

Basia: P.S. szkoda, że od razu nie napisałeś, że to gimnazjum nie pchałabym się w funkcje trygonometryczne i byłoby szybko pozdrawiam

Mexx: Dzięki wielkie , nie wiedziałem że to się przyda