Obracanie wielokątów Olek: W trójkącie ABC dane są: |AB|=c, |∡ CAB|=alfa, |∡ ABC|=beta gdzie beta<90 stopni. Oblicz objętość bryły otrzymanej w wyniku obrotu trójkąta ABC wokół prostej zawierającej wysokość poprowadzoną z wierzchołka C. Nie bardzo wiem jak to namalować. Czy mógłby mi ktoś pomóc?

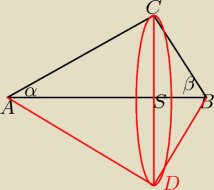
Basia: to jest suma dwóch stożków sklejonych podstawami stożek 1 r₁=CS=r h₁=AS stożek 2 r₂=CS=r h₂=BS h₁+h₂=c

	r
tgα=
	h1

	r
h1=
	tgα

	r
tgβ=
	h2

	r
h2=
	tgβ

r		r
	+		=c /*tgα*tgβ
tgα		tgβ

r*tgβ+r*tgα=c r(tgα+tgβ)=c

	c
r =
	tgα+tgβ

	c
h1=
	tgα(tgα+tgβ)

	c
h2=
	tgβ(tgα+tgβ)

teraz wystarczy policzyć V₁ i V₂ i dodać

Tomek: zły rysunek, kąt beta ma być rozwartokątny, a to zupełnie zmienia postać rzeczy, wyjdzie inna bryła

Aga1: Rysunek źle, bo ICSI ma być wysokością stożka, ale β<90⁰−−−jest to kąt ostry , więc dobrze zaznaczony.