ctgx Dziama: Prosze pomozcie!:(:(:(:(:( |ctgx|>0

Godzio: |ctgx| > 0 ⇔ ctgx ≠ 0

Dziama: ii to jest rozwiazanie?

Godzio: To ty powinieneś wiedzieć , trzeba jeszcze dokończyć ctgx ≠ 0

	π
x ≠		+ kπ
	2

Teraz podaj odpowiedź

Dziama: bo generalnie w odpowiedziach jest jakis wynik z kosmosu ja to bym zrobila tak ze narysowala bym wyjres ctg x pootem przeksztalciala o wartosc bezwzgledna i napisala w jakich przezdialach jest to wieksze od zera..ale czy to jest dobrze? nie wiem i moze ktos mi powie?

Godzio: Odp powinna być taka:

	π
x ∊ R − {		+ kπ, kπ} −− kπ wynika z dziedziny ctgx
	2

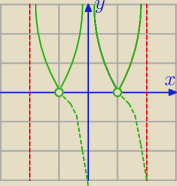Godzio: Jak widać rozwiązanie jest spełnione tylko bez punktów,

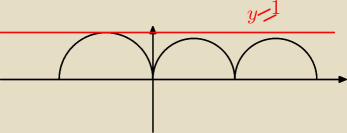Dziama: czyli mozna w taki sposob rozwiazywac? a np |sinx|<1 czyli jakie tu bedzie rozwiazanie? znaczy odp? ze x∊R?

Godzio: |sinx| < 1 ⇔ sinx ≠ 0 ⇒ x ≠ ... −− dokończ x ∊ R − {....}

Godzio: Można każdym sposobem, ważne żeby był poprawny,

Dziama:

	(2k+1)π
Ja bym powiedziała, ze −{kπ}.. ale w odpowiedziach jest ..{		} czyli to
	2

kπ+^π₂..ale nie wiem czemu to ^π₂ A no i jeszcze mam prosbe czy bys mi mogl powiedziec jak rozwiazac takie cos: tg(2x−1)≤√3

Godzio:

	π
sinx = 0 dla x =		+ kπ stąd
	2

w tg ma na pewno być −1 ? bo dziwnie wyjdzie ale jak tak ma być to zaraz rozpiszę

Dziama: Aha czyli tak jest zawsze..czyli trzeba pamietac, ze sinx=0 dla x=^π₂+kπ tak tam ma byc −1.

Godzio: Założenie:

	π		π		1		π
2x − 1 ≠		+ kπ ⇒ x ≠		+		+		* k k ∊ C
	2		4		2		2

tg(2x − 1) ≤ √3 Najpierw znajduję punkt przecięcia:

	π
2x − 1 =		+ kπ
	3

	π
2x =		+ 1 + kπ
	3

	π		1		π
x =		+		+		* k
	6		2		2

	π		1		π
Asymptotą (wartość do której dąży) są proste x =		+		+		* k
	4		2		2

więc rozwiązanie będzie

	π		1		π		π		1		π
x ∊ <		+		+		* k,		+		+		)
	6		2		2		4		2		2

Godzio:

	π
w odp, na końcu		* k
	2

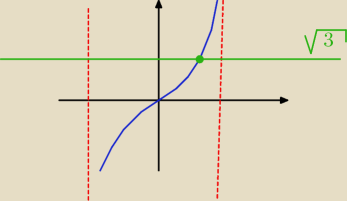Godzio: Tak to będzie wyglądać miej więcej graficznie, lepiej widać dlaczego tak a nie inaczej

Dziama: a to co wyszlo jest rowne temu? x=2π(1+4k) v x=4π(1+2k) ? jak narazie to nic nie rozumie, sprobuje przeanalizowac..i moze zrozumiembo strasznie bym chciala:( a czy moglbys jeszcze mi powiedziec choc jak rozwiazac jeszcze takie cos: sin²3x−√2sin3x+¹₂=0 podstawic za sin3x=t czy coa innego? bo tamto nie bardzo prowadzi mnie do rozwiazania. OBIECUJE ZE TO JUZ OSTATNI PRZYKLAD juz wiecej nie bede meczycpostaram na podstawie tych zrobic

Godzio: a sorki to ma być mniejsze od tego w takim razie na odwrót ta odpowiedź

Dziama: Dziękuję bardzo!

Godzio: spoko, trygonometria to mój ulubiony dział

	1
sin23x − √2sin3x +		= 0 sin3x = t , t ∊ <−1,1>
	2

	1
t2 − √2t +		= 0 −− rozwiązujemy równanie kwadratowe
	2

	√2
(t −		)2 = 0 −− zauważamy że to wzór skróconego mnożenia lub liczymy deltę i tak
	2

dalej

	√2		√2
t =		⇒ sin3x =
	2		2

	π		3π
3x =		+ 2kπ lub 3x =		+ 2kπ
	4		4

x = ... lub x = ...

Godzio: Jeszcze co do tg, to sprostowanie, rozwiązanie jest od pierwszej asymptoty do punktu przecięcia więc dokładnie rozwiązanie powinno wyglądać tak:

	π		1		π		π		1		π
x ∊ (−		+		+		* k,		+		+		* k >
	4		2		2		6		2		2

Dziama: a moja zmora a spr z calego dzialu juz za tydzien:( Dobrze, ze isteniaja tacy pomocni ludzie Skoro ulubiony dział to moze jeszcze jedno pytanie Gdy mam cos takiego: √4cos²x+4cosx+1=1 to ja sobie moge obustronnie podniesc do kwadratu i rozwiazac zwyczajnie jak rownanie kwadratowe czy to jest blad?

Godzio: Pod pierwiastkiem aż bije po oczach wzór skróconego mnożenia √(2cosx + 1)² = 1 pamiętam że √a² = |a| |2cosx + 1| = 1 2cosx + 1 = 1 lub 2cosx + 1 = −1 2cosx = 0 lub 2cosx = −2 cosx = 0 lub cosx = −1 Potrafisz to już dalej rozwiązać ?

Dziama: Oki to z sin3x juz rozumiem DZIEKUJE!teraz jeszcze tg tzreba

Godzio: Takie podstawowe dobrze żebyś kojarzyła,

	π
sinx = 1 ⇒ x =		+ 2kπ
	2

sinx = 0 ⇒ x = kπ

	π
sinx = −1 ⇒ x = −		+ 2kπ
	2

cosx = 1 ⇒ x = 2kπ

	π
cosx = 0 ⇒ x =		+ kπ
	2

cosx = −1 ⇒ x = π + 2kπ

Dziama: tak tak dalej potrafie bo to juz prosteale powiem Ci, ze wyszlo mi to samo

Godzio: To z podniesieniem do kwadratu też jest dobre ale dłuższe chyba

Dziama: Oki Niektóre z nich już nawet pamietam Dziękuję serdecznie za pomoc jeszcze raz!

Dziama: Kurcza, mam pytanie jeszcze co do jednego..tym razem naprawde ostatnie. |3tg2x|=√3 Ale tu tylko pytanie. Czy moge to powiedzielic przez 3?

Godzio: Musisz Pamiętaj o definicji wartości bezwzględnej : |x| = a ⇔ x = a lub x = −a

	π
i o dziedzinie 2x ≠ kπ ⇒ x ≠		* k
	2

Dziama: OKI CZYLI JUZ WSZYSTKO ROZUMIEM Dziękuję Godzio