. Max: FUNKCJA KWADRATOWA 1.Sporządź wykres funkcji danej wzorem f(x)=x²−x−6 2.Wyznacz przedziały monotoniczności funkcji f(x)−3x²−6x+2 3.Zbiorem wartości funkcji y=x²−6x+11 jest: A (−∞,2> B (−∞,3> C <3,∞) D <2,∞) 4.Rozwiąż nierówność−2x²+5x−2≥0 5.Wykresem funkcji f(x)=x²+Bx+c jest parabola o wierzchołku W(2,4). Wyznacz współczyniki b i c.

wx99: 1. Liczysz delte: Δ= 1+24=25 (delta >0 => dwa pierwiastki) ; √Δ=5 x1: ^−b+√Δ_2a=¹⁺⁵₂=3 x2: ¹⁻⁵₂= −2 Pięknie,ale to pięknie rysujesz wykres takiej funkcji. Pamiętaj że przy współczynniku a>0 ramionka w górę. 2.Liczysz delte, i rysujesz sobie wykres tak jak w zad.1 z tym że patrząć na wykres, zauważ gdzie jest funkcja rosnąca a gdzie jest malejąca. 3. D) Szukasz wierzchołka danej paraboli, czyli: p=^−b_2a=3 = x(pierwsza współrzędna wierzchołka; q=^−Δ_4a=2 = y(druga współrzędna; czyli w punkcie P=(3,2) znajduje się wierzchołek. Jak wiesz zbiór wartości y to po prostu druga współrzędna punktu czyli 2. Co nam daje przedział od 2 do +∞ 4. −2x² +5x −2≥0 Δ=9 −> √Δ=3 x1=¹₂ ; x2=2 Rysujesz wykres :

Max: Dziękuje bardzo

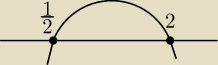
wx99: w punktach zamalowujesz kropy i na koniec piszesz x∊(−∞; ¹₂> u <2; +∞) 5. Wykorzystujesz podane wyżej wzory na p i q punkty wierzchołka. podstawiasz za x dwa, a pod y cztery co Ci daje coś takiego: p=^−b_2a 2=^−b₂ b=−4 q=^−Δ_4a 4={−Δ}{4} (dzielisz stronami przez −1) Δ=−16 masz wyliczone b i deltę, aby obliczyc podstawiasz: Δ=b² −4ac −16=(−4)² −4c −16=16 − 4c 4c=32/4 c=8 dla estetyki: f(x)=x²−4x +8

wx99: W zadaniu 4 oczywiście chodzi o wartości mniejsze bądź równe 0, źle spojrzałem na znak , w takim wypadku będzie to: (góre zamalowywujesz) x∊<¹₂;2>