dwusieczne Michal: Znaleźć równania dwusiecznych kątów wyznaczonych przez proste o równaniach 3x+4y−2=0 4x−3y+5=0

Basia: dwusieczna to zbiór punktów równo odległych od ramion kąta P(x₀,y₀)

	|3x0+4y0−2|		|3x0+4y0−2|
d1=		=
	√9+16		5

	|4x0−3y0+5|		|4x0−3y0+5|
d2=		=
	√16+9		5

d₁=d₂ stąd |3x₀+4y₀−2| = |4x₀−3y₀+5| wskaźnik można opuścić mamy: 3x+4y−2=4x−3y+5 lub 3x+4y−2=−(4x−3y+5) −x+7y−7=0 lub 7x+y+3=0 i to wszystko

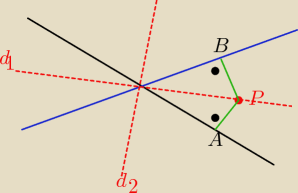
domino: z definicji dwusiecznej odległości punktu P(x,y) od tych prostych są równe bo punkt leżący na dwusiecznej kąta jest równo odległy od ramion tego kąta

	|3*x+4*y−2|		|4*x−3*y+5|
zatem		=
	√32+42		√42+(−3)2

otrzymasz |3x+4y−2|= |4x−3y+5| z równań : d₁: 3x+4y −2= 4x−3y+5 d₂: 3x+4y −2= −4x+3y −5 otrzymasz równania obydwu dwusiecznych dokończ............

domino: Echhhh Basiu Co to znaczy "młodość" ( znów się spóźniłam )

Basia: Michał ma jeszcze jedno zadanie, to z podziałem płaszczyzny przez proste; za diabła nie mogę sobie przypomnieć jak to ugryźć