wartość bezwględna xman: równanie postaci |x−a| = c, którego rozwiązaniami są liczby 3 i 10

mac: Najłatwiej chyba: https://matematykaszkolna.pl/strona/1093.html

Basia: c≥0 |x−a|=c ⇔ x−a=c lub x−a=−c ⇔ x=a+c lub x=a−c stąd a+c=10 a−c=3 −−−−−−−−−−−−−−− 2a=13 a=¹³₂ a+c=10 c=10−a c=²⁰₂−¹³₂ = ⁷₂ lub a+c=3 a−c=10 −−−−−−−−−−−−−−−−− 2a=13 a=¹³₂ a+c=3 c=3−a c=⁶₂−¹³₂=−⁷₂ odpada bo jest <0 czyli a=¹³₂ c=⁷₂ czyli |x−¹³₂|=⁷₂

bajka:

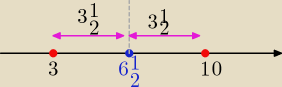
	x1+x2		3+10
a=		=		= 612
	2		2

c= 10−6¹₂= 3¹₂ c= 6¹₂−3= 3¹₂ |x − 6¹₂ |= 3¹₂

xman: Aha, czyli trzeba było zrobić dwa układy równań A takie coś? nierówność postaci |x−a| < c, której zbiorem rozwiązań jest (−π+2; π−4).