Pomóżcie Ola: W okrąg o środku O wpisano czworokąt ABCD. Wyznacz miary kątów tego czworokąta oraz miarę kąta ostrego utworzonego przez jego przekątne, jeśli: a) |∡AOB|=120 |∡BOC|=120 |∡COD|=40 b) |∡AOB|=150 |∡AOD|=60 |∡COD|=70

think: co musi spełnić czworokąt aby można go było wpisać w okrąg?

think: przede wszystkim zrób rysunek i zaznacz to co masz podane...

Ola: Ale nadal nie wiem jak to zrobic

think: zrób rysunek.

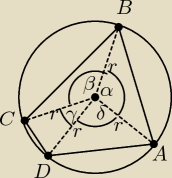
think: rysunek ogólny dwa obu podpunktów. trzeba wiedzieć dwie rzeczy: α + β + γ + δ =360^o oraz, że trójkąty złożone z dwóch wierzchołków czworokąta i środka okręgu są trójkątami

	180 − δ
równoramiennymi, więc np w trójkącie ODA kąty ODA i OAD są równe i wynoszą po
	2

Ola: No dobrze ale co dalej zrobic ? Niestety jestem noga z matmy i nie wiem co dalej.

think: Ola masz podane kąty... AOB = 120^o

	180 − 120
więc kąty przy podstawie mają po		= 30o
	2

pozostałe liczysz tak samo i zaznaczasz na rysunku...

Ola: Dobra dzięki. Naprawdę dużo mi pomogłeś. Wielkie dzięki

Barni: nie ma sprawy