W trójkącie równobocznym magda: W trójkącie równobocznym ABC dane są wierzchołki A = (−2, −1) i B= (2, −1), Trzeci wierzchołek o drugiej współrzędnej dodatniej ma współrzędne

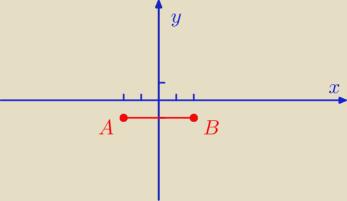
Godzio: |AB| = 4

	4√3
h =		= 2√3
	2

C(0,y), y > 0 Odległość C od prostej y = −1 ⇒ y + 1, która zawiera bok AB ma długość 2√3

	|y + 1|
d =		= 2√3
	√02 + 12

|y + 1| = 2√3 y = 2√3 − 1 lub y = −2√3 − 1 y > 0 Odp: C(0, 2√3 − 1)

Gustlik: Można troszkę prościej: wystarczy zauważyć, że mamy do czynienia z prostą "poziomą" y=−1, a więc wystarczy do y=−1 dodać wysokość trójkąta i wyjdzie współrzędna y punktu C, czyli będzie to 2√3−1. Ten wzór na odległość punktu od prostej jest doskonały, gdy liczy się odległość punktu od prostej "skośnej". Pozdrawiam