lb KM: Wyznacz równanie wektorowe prostej 2x+3y=5. Nie wiem jak to zrobić, niestety nie mieliśmy tego na wykładzie

KM: Może ktoś ma jakiś pomysł?

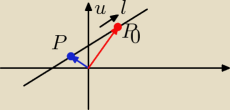
Mateusz: Nie było nic na wykłądzie a dali wam do domu no co za nauczyciele równanie wektorowe prostej l mozemy wyrazic tak: l: OP=OP₀+t*u l−prosta przechodząca przez punkt P₀ i równoległa do niezerowego wektora u

KM: Mieliśmy tylko równanie prostej, jak mamy podany wektor albo przechodzącej przez 2 pkt, ale nie zrobiliśmy żadnego przykładu, jak jest x i y. No ale ten punkt to (2,5) a wektor 5? Bo nie wiem jak się mają x i y do tego wzoru.

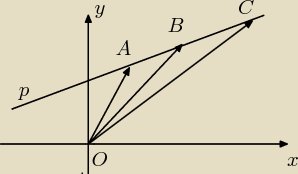
AS: Niech będzie dana prosta p i dwa różne punkty A(x1,y1) i B(x2,y2) na niej położone. Tworzę wektory → → → OA = [x1,y1] , OC = [x,y] , AB = = [ax,ay] gdzie ax = x2 − x1 , ay = y2 − y1 Z reguły dodawania wektorów mamy → → → → → OC = OA + AC = OA + k*AB gdzie k ∊ R Wyrażając wektory przez współrzędne mamy równanie wektorowe prostej [x,y] = [x1,y1] + k*[ax,ay] W podanym przykładzie mamy dane: prosta 2x + 3y = 5 Obieram dwa punkty prostej np. A(1,1) , B(4,−1) Wtedy ax = 4 − 1 = 3 , ay = −1 −1 = −2 Równanie wektorowe prostej: [x,y] = [1,1] + k*[3,−2] , k ∊ R dla k = 0 mamy [x,y] = [1,1] czyli punkt A(1,1) dla k = 10 mamy [x,y] = [31,−19] czyli pewien punkt prostej D(31,−19)