
 , które z odcinków |AB| |BC| |CD| czy |AD|
, które z odcinków |AB| |BC| |CD| czy |AD|
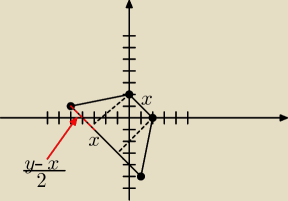 natomiast wysokość liczysz z tw pitagorasa
natomiast wysokość liczysz z tw pitagorasa
| dł.podstawy dłuższej − dł.podstawy krótszej | ||
h2 + ( | )2 = (dł.ramienia)2 | |
| 2 |

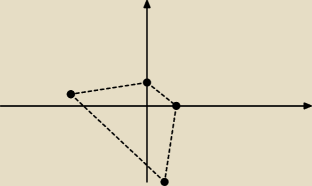 1. Narysuj to w układzie współrzędnych
2.oblicz środki odcinków CD i AB XśrAB=[1+(−5)]/2=−2 Yśr AB=(−5+2)/2=−2
XśrCD=(2+0)/2=1 Yśr CD=(0+2)/2=1
3. Równanie prostej przechodzącej przez punkty (−2,−2) i (1,1) otrzymasz po rozwiązaniu układu
równań: −2=−2a+b
1= a+b bo a= 1 b=0 a więc równanie prostej, która jest osią symetrii: y=x
4 Pole: Dł. AB= 6√2. Dł. CD=2√2 Wysokość(środki AB i CD)=3√2
P=[(6√2+2√2)*3√2]/2=24 jedn. kwadratowe
1. Narysuj to w układzie współrzędnych
2.oblicz środki odcinków CD i AB XśrAB=[1+(−5)]/2=−2 Yśr AB=(−5+2)/2=−2
XśrCD=(2+0)/2=1 Yśr CD=(0+2)/2=1
3. Równanie prostej przechodzącej przez punkty (−2,−2) i (1,1) otrzymasz po rozwiązaniu układu
równań: −2=−2a+b
1= a+b bo a= 1 b=0 a więc równanie prostej, która jest osią symetrii: y=x
4 Pole: Dł. AB= 6√2. Dł. CD=2√2 Wysokość(środki AB i CD)=3√2
P=[(6√2+2√2)*3√2]/2=24 jedn. kwadratowe
| yB−yA | −6 | |||
a= | = | =−1 − można tu skorzystać z własności, że jeżeli prosta jest | ||
| xB−xA | 6 |
| wy | ||
a= | . Tym wektorem jest AB→.
| |
| wx |
| |AxC+ByC+C| | ||
h= | , C=(2;0)
| |
| √A2+B2 |
| |2+0+4| | 6 | 6√2 | ||||
h= | = | = | =3√2
| |||
| √12+12 | √2 | 2 |
| (a+b)*h | ||
Pole P= | ||
| 2 |
| (6√2+2√2)*3√2 | 8√2*3√2 | 24*2 | ||||
P= | = | = | =24
| |||
| 2 | 2 | 2 |
 " z rys. widać, że podstawami są AB i CD i trapez jest równoramienny"
a co będzie? jak punkty będą mieć współrzędne np: A( 120, −250) ......
" z rys. widać, że podstawami są AB i CD i trapez jest równoramienny"
a co będzie? jak punkty będą mieć współrzędne np: A( 120, −250) ......  nic z rysunku nie można obliczać!
zatem tak:
→ →
AB= [6, −6] i DC= [ 2,−2] co oznacza,że IABI= 3*IDCI
i wektory AB i DC są równoległe, bo 6*2 −(−6)*(−2) = 0 −−− warunek równoległości
zatem AB i DC są podstawami trapezu
to: IABI= √62+(−6)2= √2*36= 6√2
IDCI= √(22 + (−2)2= √2*4= 2√2
teraz sprawdzamy, czy trapez jest równoramienny
IADI = IBCI = √52+12= √26 −−− zatem trapez jest równoramienny
wniosek ,że środki E i F podstaw AB i DC
wyznaczają h= IEFI
E( −2,2) i F( 1,1)
zatem oś symetrii to prosta EF : y= x
i h= IEFI= √(1+2)2 + ( 1+2)2= √2*9= 3√2
i mamy wszystko do wyznaczenia pola trapezu:
nic z rysunku nie można obliczać!
zatem tak:
→ →
AB= [6, −6] i DC= [ 2,−2] co oznacza,że IABI= 3*IDCI
i wektory AB i DC są równoległe, bo 6*2 −(−6)*(−2) = 0 −−− warunek równoległości
zatem AB i DC są podstawami trapezu
to: IABI= √62+(−6)2= √2*36= 6√2
IDCI= √(22 + (−2)2= √2*4= 2√2
teraz sprawdzamy, czy trapez jest równoramienny
IADI = IBCI = √52+12= √26 −−− zatem trapez jest równoramienny
wniosek ,że środki E i F podstaw AB i DC
wyznaczają h= IEFI
E( −2,2) i F( 1,1)
zatem oś symetrii to prosta EF : y= x
i h= IEFI= √(1+2)2 + ( 1+2)2= √2*9= 3√2
i mamy wszystko do wyznaczenia pola trapezu:
| 6√2+2√2 | ||
P= | *3√2= 4√2*3√2= 24 [j2]
| |
| 2 |

 ? Gdyby babcia miała wąsy, to by była dziadkiem. Jest konkretne
zadanie − z rysunku można wiele odczytać, więc korzystam z tego. Poza tym można zmienić skalę
na osiach, przyjąć, że jedna kratka to 10 albo 20 i też się da zauważyć. Poza tym jest to do
sprawdzenia − wystarczy obliczyć długości ramion trapezu znając współrzędne wierzchołków.
Pozdrawiam
? Gdyby babcia miała wąsy, to by była dziadkiem. Jest konkretne
zadanie − z rysunku można wiele odczytać, więc korzystam z tego. Poza tym można zmienić skalę
na osiach, przyjąć, że jedna kratka to 10 albo 20 i też się da zauważyć. Poza tym jest to do
sprawdzenia − wystarczy obliczyć długości ramion trapezu znając współrzędne wierzchołków.
Pozdrawiam 
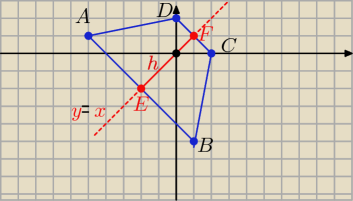 I teraz mozemy sprawdzić rozwiazanie nanosząc współrzędne w układzie
bo przy takich współrzędnych da się to wykonać
jak widać na załączonym "obrazku" wszystko "gra i buczy"
I teraz mozemy sprawdzić rozwiazanie nanosząc współrzędne w układzie
bo przy takich współrzędnych da się to wykonać
jak widać na załączonym "obrazku" wszystko "gra i buczy" 
 E( −2, −2)
E( −2, −2)
 To przynajmniej przyznaj rację,że
h= IEFI
po co zatem wprowadzać niepotrzebne obliczenia do wyznaczenia długości h
To przynajmniej przyznaj rację,że
h= IEFI
po co zatem wprowadzać niepotrzebne obliczenia do wyznaczenia długości h

 !
!