monotoniczność funkcji aga: Proszę o sprawdzenie Wyznacz przedziały monotoniczności funkcji: przykład b)

	x
f(x) =
	1+x2

	(x)' * (1+x2) − x * (1+x2)'		1*(1+x2)−x*2x
f ' (x) =		=		=
	(1+x2)2		(1+x2)2

	1+x2−2x2		−x2+1
=		=
	(1+x2)2		(1+x2)2

liczę dla y=−x²+1 Δ=4 W(p,q)

	−b		−Δ
p=		= 0 q=		= 1
	2a		4a

W(0,1) funkcja rosnąca (−∞;0) funkcja malejąca (0,+∞)

Bogdan: a po co Δ? −x² + 1 = −(x² − 1) = −(x − 1)(x + 1)

Bogdan: a przedziały monotoniczności są inne

aga: a teraz jest dobrze? f'(x) > 0 ⇔ (−1,1) f'(x) < 0 ⇔ (−∞;−1) ∪ (1;+∞)

aga: chociaż myslę, że powinno być: funkcja rosnąca (−∞;0 > funkcja malejąca <0,+∞)

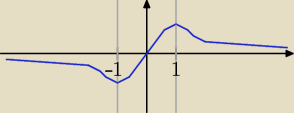
Bogdan: To jest szkic wykresy tej funkcji

Bogdan: Funkcja y = f(x) jest malejąca w zbiorze A, wtedy gdy dla dowolnych x₁, x₂ ∊ A z warunku; x₂ − x₁ > 0 wynika, że f(x₂) − f(x₁) < 0. Funkcja y = f(x) jest rosnąca w zbiorze A, wtedy gdy dla dowolnych x₁, x₂ ∊ A z warunku; x₂ − x₁ > 0 wynika, że f(x₂) − f(x₁) > 0. Podałem definicję funkcji malejącej w zbiorze A i definicję funkcji rosnącej w A.

	x
Niech f(x) =		oraz A = (−∞, −1)∪(1, +∞)
	1 + x2

Weźmy dwa dowolne punkty z tego przedziału, np. x₁ = −2, x₂ = 2.

	−2
f(x1) = f(−2) =
	5

	2
f(x2) = f(2) =
	5

	2		−2		4
Otrzymujemy: f(x2) − f(x1) =		−		=		> 0, co oznacza, że w przedziale
	5		5		5

A = (−∞, −1)∪(1, +∞) funkcja jest rosnąca, co jak widać na szkicu, nie jest prawdą. Gdzie jest więc ago nieścisłość w stwierdzeniu: funkcja jest malejąca dla x ∊ (−∞, −1)∪(1, +∞)