Równanie okręgu Sylwia: Napisz równanie okręgu przechodzącego przez punkt A i stycznego do obu osi układu współrzędnych, jeśli: a) A(2,0) b) A(0,3) Do każdego przykładu są po dwie odpowiedzi, a mi wychodzi, że jest tylko jedno równanie na jeden przykład. Dlaczego?

Marcin: pokaż jak rozwiązujesz.

Sylwia: a) A(2,0) S(a,b) B(a,0) C(0,b) a=b=r (2−a)²+a²=a² a²−4a+4=0 Δ=16−16=0 stąd wychodzi, ze jest tylko jedno rozwiazanie i a=2, czyli równanie okręgu to: (x−2)²+(y−2)²=4. W odpowiedziach są dwa rozwiazania. To i to: (x−2)²+(y+2)²=4. Dlaczego?

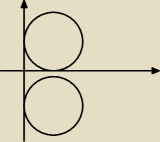
Marcin: dlatego tak masz(jedna odp) że zakładasz tylko że a=b popatrz na nieudolny rysunek a może być a=−b

Sylwia: Ale te same założenia miałam do A(2,1) i A(1,2) i wyszly mi dwa rownania okregow.

Sylwia: Jeśli założe, ze a=b ∨ a=−b to w pozostałych podpunktach wyjda mi 4 rozwiazania zamiast 2

Sylwia: Dobra juz wiem o co chodzi

Marcin: oki po kolei 1) więc założyłaś ze a=b czyli mamy do czynienia z okręgiem górynym na moim nieudolnym obrazku powyżej: bo założyłaś że obie współrzędne środka okręgu są dodatnie jasne ? Skoro tak to r=a=b ok zgoda masz równanie okręgu : (x−a)²+(y−b)²=r² Podstawiamy współrzedne punktu przez które okrag przechodzi czyli (2,0) (2−a)²+a²=a² i dalej masz że a= 2 wsio ok 2) Załóżmy teraz drugi przypadek a=−b, r=a oraz a>0 (promien musi byc dodatni) mamy: (2−a)²+a²=a² czyli to samo rozwiązanie co w przypd 1 czyli a=2 a skoro zalozylismy ze a=−b zatem b=−2 co daje wsp srodka drugiego okręgu S(2,−2) i odp z ksiazki.