trójąt,okrąg wpisany i opsiany katarzyna21: Boki trójkąta mają dłAB|=4 |AC|=|BC|=8.Oblicz długości promieni okręgów wpisanego w trójkąt ABC i opisanego na nim

Marcin: Policz pole trójkata wykorzystujac Pitagorasa a potem wylicz R z gotowych wzorów

Grześ: nie ma podane, że to prostokątny, jak chcesz to policzyć Chyba, że treśc zadania niezupełna

Grześ: aaa, dobra, sorry, nie zauważyłem jednego szczegółu, przepraszam. Bo ta minka mnie rozprasza

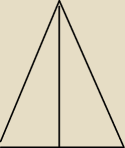
Marcin: Tórjkat rownoramienny jego wysokosc podzieli podstawe na dwa równe odcinki bedą dwa prostokątne i tam Pitagoras do wyliczenia wysokosci trójkata ...

Grześ: tak, tak, zauważyłem to od razu po napisaniu postu. Jest ok

Marcin: wiem od początku ze jest ok

Grześ: tak, tak, to dobrze

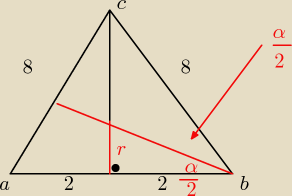
TOmek: 64=16+64−64cosα cosα=0,25≈=75^o cos75^o

	1
P=		2*8sin75≈7,72
	2

	2P
r=
	a+b+c

	abc
R=
	4P

wiem ,ze jest to trudniejsza metoda, ale moje pytanie brzmi czy w taki sposob takze moze byc to rozwiązane

katarzyna21: Z Pitagorasa obliczyłam wysokość/ TEraz do wzoru na okrąg opisany: R=a*b*c/4P

katarzyna21: Potrzebuje najprostszej metody.

Marcin: Tomek wyznaczasz z cosinusa kat który jest tylko przybliżeniem. Stąd nie rowzwiązywałbym tego w podany przez ciebie sposób. Chyba że wynik też ma być przybliżony. Katarzyna wyliczyłaś wysokość to teraz pole oblicz tego trojkata i dalej do wzoru ktory podalas.

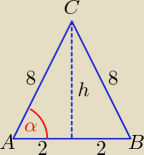
Bogdan: R − długość promienia okręgu opisanego. h = √64 − 4 = √60 = 2√15

	2√15
sinα =		,
	8

	|BC|
Na podstawie twierdzenia sinusów:		= 2R ⇒ R = ...
	sinα

katarzyna21: P=a*h/2 P=4*2{15}/2 P=4{15}