... Anna: Obrazem odcinka AB, gdzie A=(1,0) i B=(2,1) w jednokładności o skali k>1 i środku P jest odcinek CD, gdzie C=(4,0), D=(6,2). Zapisz równanie okręgu o środku w punkcie P i promieniu |AB|.

Anna: wiem,że to może sprawić problem,ale błagam o pomoc... sama sobie z tym nie poradzę

sushi_ gg6397228: zrob rysunek jaki jest wzor na jednokladnosc

Anna: wzór na jednokładność: J_o^s(x,y)=(x',y') {x'=s*x {y'=s*y o ten wzór chodzi?

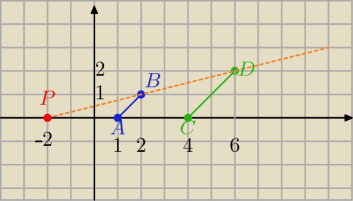
Eta: skoro skala k>1 to odcinki AB i CD leżą po jednej stronie → → PC = k* AC

	|CD|
k=
	|ABI

|CD| = √2²+2²= √8= 2√2 |AB|= √1²+1² = √2

	2√2
to k=		= 2
	√2

→ → zatem: PC= 2*AC → → PC= [ x_C − x_P, y_C−y_P] AC= [ x_C−x_A, y_C − y_A → → → PC= [ 4−x_P, 0−y_P] AC= [ 3, 0] to 2*AC= [6,0] to 4−x_P= 6 i y_P= 0 x_P= −2 i y_P= 0 P(−2,0) P= S( −2,0) r= |AB|= √2 to r²= 2 o: ( x+2)² +y²= 2 ]

sushi_ gg6397228: z rysunku widac ze skala jest 2 tylko z tym punktem cos nie tak

Eta: sushi w którym miejscu jest ......."z tym punktem coś nie tak" ?