Prawdopodobieństwo-roz. Kasia-Rz: Wśród dziesięciu osób pięć zna język angielski, siedem język niemiecki i sześć osób zna francuski, przy czym każda z osób zna przynajmniej jeden z tych języków. Oszacuj prawdopodobieństwo, że losowo wybrana osoba zna trzy języki. Odpowiedz w książce jest taka 0<=P(A)<=0,4

Kasia-Rz: Hej, jest tam kto?

sushi_ gg6397228: policz ile jest wszystkich osob co zna jezyki 5+7+6=... potem trzeba narysowac trzy zbioru i popatrzec jaka bedzie czesc wspolna

Kasia-Rz: Osób jest 10. Nie wiem o co chodzi w tym zadaniu. Bardzo proszę o rozpisanie I bez zbiorów miało być to rozwiązanie.

sushi_ gg6397228: (...)pięć zna język angielski, siedem język niemiecki i sześć osób zna francuski,(...) ile masz osób

Kasia-Rz: No osób jest 10 przecież. I w tych 10 jest np. jedna co zna 3 języki. Nie rozumiem do czego zmierzasz.

sushi_ gg6397228: masz policzyc ile jest osob w poscie o 23.23

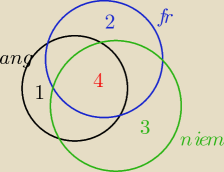
Eta: skoro każda osoba zna przynajmniej jeden język to P(A) >0 to na rys. jest maxymalna opcja A −−−− co najwyżej 4 osoby mogą znać trzy języki

	4
P(A) ≤		= 0,4 i P(A) >0
	10

0< P(A) ≤ 0,4

Kasia-Rz: 5+7+6=18. I co z tego?

sushi_ gg6397228: to znaczy ze 8 osob musi uczyc sie przynajmniej dwóch języków

Kasia-Rz: Wcale nie, właśnie o to chodzi. Popatrz na graf Eta. Czy da się to jakoś rozpisać z działań na zbiorach?

wojtek46656: Niech A − zbiór osób znających angielski, B − zbiór osób znających niemiecki, C − zbiór osób znających francuski Niech x oznacza liczbę osób znających 3 języki. Wtedy (10−x) osób zna co najwyżej 2 języki. Pierwsze spostrzeżenie: wśród osób znających co najwyżej 2 języki są: − osoby z A nieznające 3 języków (5−x) − osoby z B nieznające 3 języków (7−x) − osoby z C nieznające 3 języków (6−x) Zatem (10−x) ≤ (5−x) + (7−x) + (6−x) Stąd: 2x ≤8, czyli x ≤ 4 Drugie spostrzeżenie: wśród osób znających co najwyżej 2 języki są: − osoby nieznające angielskiego (10−5), − osoby nieznające niemieckiego (10−7), − osoby nieznające francuskiego (10−6). Zatem (10−x) ≤ (10−5) + (10−7) + (10−6) Stąd: x ≥ −2 (nierówność 1) Ponieważ x naturalne, mamy: 0 ≤ x ≤ 4 Prawdopodobieństwo, że losowo wybrana osoba zna trzy języki, to x/10. Dzieląc przez 10 strony nierówności 1 otrzymujemy: 0 ≤ x/10 ≤ 0,4 0 ≤ p ≤ 0,4