Pomocy Blondi: W równoległoboku ABCD z wierzchołka D kąta rozwartego poprowadzono dwie różne wysokości DE i DF, przy czym DE ⊥ AB, DF ⊥ BC. a) Wykaż, że trójkąty AED i FCD są podobne. b) Wiedząc dodatkowo, że |AD| : |DC| = 4:5, oblicz, o ile procent wysokość DF jest dłuższa od wysokości DE.

Blondi:

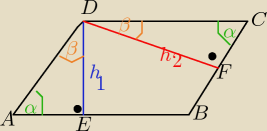
Eta: a) z cechy (k,k,k) ΔAED ~ ΔFDC bo mają po dwa kąty równe: |<EAD| = |<FCD|= α i |<AED|= |<CFD|= 90^o zatem |<ADE|= |< FDC|= β c.n.u b) ponieważ w/w trójkąty są podobne, to:

	|AD|		|DE|		4
		=		=
	|DC|		|DF|		5

	5
zatem: |DF|=		|DE|
	4

	5		1
		|DE|− |DE|=		|DE|
	4		4

	14|DE|		1
więc		*100% =		*100%= 25%
	|DE|		4

|DF| jest dłuższa od |DE| o 25%

Blondi: Wielkie dzięki