dwa styczne okregi re-up ;D pomocyyyyy
essh:
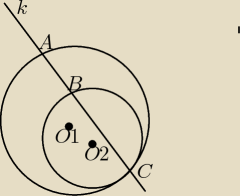
mam problem z zadaniem: Dwa styczne okręgi o środkach odpowiednio o1 i o2 przecina
prosta k przechodzaca przez punkt stycznosci C i przecinająca oba okregi w punktach A i B.
Udowodnij, że katy środkowe w obu okregach, oparte na łukach wyznaczonych przez prosta k ( nie
bedaca srednica okregow) są równe.
zakladam temat po raz drugi, w pierwszym otrzymałem odp od
Basi
CO1=AO1=r1 AC=2r1
CO2=BO2=r2 BC=2r2
CO1CO2=
BO1BO2=
BCAC=
r1r2
co wskazywało by na podobienstwo trojkątów
kat CO1B=katCO2A
nie zacytowalem zbyt dokładnie bo nie do konca rozgryzłem edytor jednak chodzi o idee, nie
mozemy stwierdzic, że BC = 2r2 bo w zadaniu jest powiedziane że prosta k nie jest srednica
zadnego z okregow, jak to jest ? ;>
18 lis 19:54
essh: nie ogarnia nikt tego ? wiedzialem ze te dowodzenie nie ludzkie jest xD
18 lis 20:14
Basia:
a masz rację; przeoczyłam, że to nie są średnice
18 lis 20:51
essh: da rade jakos inaczej to wykazac?

18 lis 20:54
karolina: kąt O1CB jest przystajacy do kąta O2CA bo to ten sam kąt , trójkaty ACO1 i BCO2 są
równoramienne ...
18 lis 20:57
Basia:
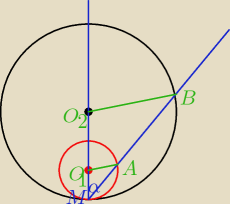
na mocy tw. odwrotnego do tw.Talesa
AO
1 || BO
2 ⇒
∡MO
1A = ∡MO
2B
zmieniłam niechcący oznaczenia, ale chyba się połapiesz
18 lis 21:00
essh: tzn ze srodki leza na jednej prostej ? przecinajacej prosta k pod jakims tam katem ?
niezaleznie od przesuuwania sb mniejszego okregu i punktu stycznosci ;> ?
18 lis 21:02
Basia:
tak, środki i punkt styczności jeżą na jednej prostej
18 lis 21:03
Basia:
tak jest zawsze, także dla zewnętrznie stycznych
18 lis 21:05
essh: elegancko

jesteś wielka

dopisze sie do listy uwielbiajacych



dzięki

18 lis 21:05
Basia:
podoba mi się też rozwiązanie karoliny
18 lis 21:09
essh: w sumie mi tez xD bo na jedno wychodzi.. ja nie wiedzialem ze one na jednej prostej leza i tak
kombinowałem brrr
karolina tez jest wielka

18 lis 21:11
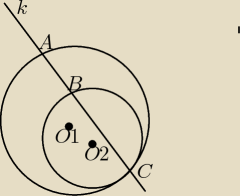 mam problem z zadaniem: Dwa styczne okręgi o środkach odpowiednio o1 i o2 przecina
prosta k przechodzaca przez punkt stycznosci C i przecinająca oba okregi w punktach A i B.
Udowodnij, że katy środkowe w obu okregach, oparte na łukach wyznaczonych przez prosta k ( nie
bedaca srednica okregow) są równe.
zakladam temat po raz drugi, w pierwszym otrzymałem odp od Basi
CO1=AO1=r1 AC=2r1
CO2=BO2=r2 BC=2r2
CO1CO2=BO1BO2=BCAC=r1r2
co wskazywało by na podobienstwo trojkątów
kat CO1B=katCO2A
nie zacytowalem zbyt dokładnie bo nie do konca rozgryzłem edytor jednak chodzi o idee, nie
mozemy stwierdzic, że BC = 2r2 bo w zadaniu jest powiedziane że prosta k nie jest srednica
zadnego z okregow, jak to jest ? ;>
mam problem z zadaniem: Dwa styczne okręgi o środkach odpowiednio o1 i o2 przecina
prosta k przechodzaca przez punkt stycznosci C i przecinająca oba okregi w punktach A i B.
Udowodnij, że katy środkowe w obu okregach, oparte na łukach wyznaczonych przez prosta k ( nie
bedaca srednica okregow) są równe.
zakladam temat po raz drugi, w pierwszym otrzymałem odp od Basi
CO1=AO1=r1 AC=2r1
CO2=BO2=r2 BC=2r2
CO1CO2=BO1BO2=BCAC=r1r2
co wskazywało by na podobienstwo trojkątów
kat CO1B=katCO2A
nie zacytowalem zbyt dokładnie bo nie do konca rozgryzłem edytor jednak chodzi o idee, nie
mozemy stwierdzic, że BC = 2r2 bo w zadaniu jest powiedziane że prosta k nie jest srednica
zadnego z okregow, jak to jest ? ;>


 jesteś wielka
jesteś wielka  dopisze sie do listy uwielbiajacych
dopisze sie do listy uwielbiajacych 

 dzięki
dzięki 
