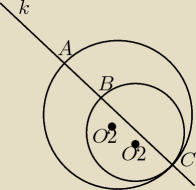
Planimetria : dwa styczne okregi... essh: Witam xd mam problem z zadaniem: Dwa styczne okręgi o środkach odpowiednio o1 i o2 przecina prosta k przechodzaca przez punkt stycznosci C i przecinająca oba okregi w punktach A i B. Udowodnij, że katy środkowe w obu okregach, oparte na łukach wyznaczonych przez prosta k ( nie bedaca srednica okregow) są równe.

essh: wytlumaczy ktos jak sie do tego zabrac ? mozna powiedziec ze beda to trojkaty podobne i dlatego katy sa takie same ? jak to uzasadnic ? ;>

Basia: można CO₁=BO₁=r₁ BC=2r₁ CO₂=AO₂=r₂ AC = 2r₂

CO1		BO1		BC		r1
	=		=		=
CO2		BO2		AC		r2

są więc z całą pewnością podobne ⇒ ∡CO₁B = ∡CO₂A

essh: ale nie mozna powiedziec ze BC=2r1 poniewaz k nie jest srednica zadnego z okregow... tzn BC lub/i AC

essh: rysunek nie jest zbyt dokladny ale w tresci jest powiedziane all i wlasnie nie jest to takie proste jak by się wydawało

essh: da się to jakos inaczej 'odswiezyc' czy tylko poprzez podbijanie postow ? xD zalezy mi na tym zadaniu a w ksiazce odp nie dali