funkcja vertical: Czy dobrze zrobione? http://images41.fotosik.pl/387/40cf7380bae3dedemed.jpg a) f. rosnąca dla x∈<−5,1> u x∈<2,4> b) ZW=(−4,4) c) f(x)>0 dla x∈(−1,2) u x∈(2,5) d) f(x)<0 dla x∈<−5,1) u x∈(5,6) e) −1,2,5 f) D=<−5,6) g) ymax=4 h) 3

Ruda: b) Zbw = ( −4 ; 4 > Ja bym tak zaznaczyła

vertical: No właśnie nad tym się zastanawiałem, no i nie wiedziałem co wstawić. Dlaczego > nie )?

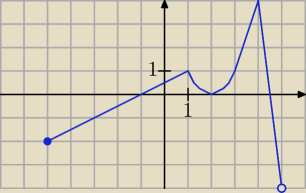
Bogdan: a) f ↗ dla x∊<−5, 1>, <2, 4>; (uwaga − błędny jest zapis <−5, 1>∪<2, 4>) b) ZW_f: y∊(−4, 4>; ( f(4) = 4, a wiec istnieje wartość funkcji równa 4) c) f(x) > 0 dla x∊(−1, 2)∪(2, 5); d) f(x) < 0 dla x∊<−5, −1)∪(5, 6); e) miejsca zerowe: x∊{−1, 2, 5}; f) D_f: x∊<−5, 6); g) y_max = 4; h) f(1) istnieje dla trzech argumentów.

Jack: z ciekawości, czemu taki zapis: x∊<−5, 1>∪<2, 4>, jest błędny?

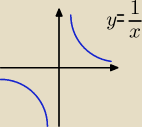
Bogdan: Wyjaśniam, dlaczego nie można stosować znaku ∪ przy opisywaniu przedziałów monotoniczności funkcji. Przypomnijmy sobie definicję funkcji rosnącej i definicję funkcji malejącej: Funkcja y = f(x) jest rosnąca w przedziale A ⇔ ⇔ dla dowolnych x₁, x₂ ∊ A: x₂ − x₁ > 0 ⇒ f(x₂) − f(x₁) > 0. Funkcja y = f(x) jest malejąca w przedziale A ⇔ ⇔ dla dowolnych x₁, x₂ ∊ A: x₂ − x₁ > 0 ⇒ f(x₂) − f(x₁) < 0.

	1
Weźmy np. funkcję f(x) =		i przedział A = (−2, 0)∪(0, 2).
	x

Niech x₁ = −1, x₂ = 1. Spełnione jest założenie; x₂ − x₁ > 0. f(x₁) = f(−1) = −1, f(x₂) = f(1) = 1. Widać, że f(x₂) > f(x₁) ⇒ f(x₂) − f(x₁) > 0, a więc f(x) jest w przedziale A rosnąca, co nie jest prawdą. Sprzeczność wynikła z błędnego przyjęcia przedziału A. Zamiast A = (−2, 0)∪(0, 2) należy przyjąć: A₁ = (−2, 0), A₂ = (0, 2). Teraz możemy dobrać x₁ i x₂ albo z przedziału A₁ albo z przedziału A₂. Dla A₁: Niech x₁ = −1, x₂ = −0,5. x₂ − x₁ > 0

	1
f(x2) = f(−0,5) =		= −2, f(x1) = f(−1) = −1.
	−0,5

Mamy więc: f(x₂) − f(x₁) < 0 co oznacza, że funkcja w przedziale A₁ jest malejąca i to jest prawda. Przy określaniu przedziałów monotoniczności nie można wstawiać znaku sumy zbiorów, bo taki zapis może prowadzić do sprzeczności. Należy stosować przecinek, tak, jak pokazałem np. w zadaniu verticala: f ↗ dla x∊<−5, 1>, <2, 4>. Przykład: http://www.adammlynarczyk.com/monotonicznoscfunkcji.html

Jack: Wielkie dzięki, Bogdanie! Faktycznie taki zapis prowadzi do nieporozumień. Prowadzi on jednak do trudności jedynie w niektórych przypadkach. Np. gdy podajemy zbiór, dla których funkcja jest monotoniczna. Gdybym jednak chciał wypisać dziedzinę, to problemu z takim zapisem by nie było. Niemniej, wielkie dzięki za tak obszerne wyjaśnienie (nie zdawałem sobie sprawy z istnienia problemu).