Jasio: Potrzebuje pomocy z następujących zadaniach: 1.W trójkąt o podstawie długości 10 i wysokości długości 6 poprowadzonej do podstawy wpisano prostokąt tak, że jeden z jego boków zawiera się w podstawie. Oblicz maksymalne pole P prostokąta. 2. Wykaż, że suma długości średnic okręgu opisanego i okręgu wpisanego w trójkąt prostokątny jest równa sumie długości jego przyprostokątnych.

Godzio: 2.

	a + b − c
r =
	2

	1
R =		c
	2

d₁ + d₂ = 2r + 2R = a + b − c + c = a + b

Jasio: Wielkie dzięki za to zadanie!

Jasio: Pomoże ktoś z tym pierwszym zadaniem?

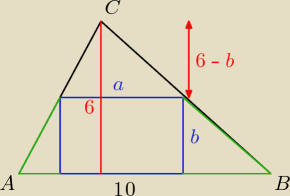
Godzio: Łączę sobie sobie 2 zielone trójkąty i powstaje mi jeden o podstawie 10 − a i wysokości b

	a		6 − b		5
Z podobieństwa:		=		⇒6a = 60 − 10b ⇒ a = 6 −		b
	10		6		3

Żeby pole prostokąta było największe suma pól 2 trójkątów musi być najmniejsza

	a(6 − b)		b(10 − a)
P1 + P2 =		+		= minimum − podstaw a i wylicz wierzchołek bw
	2		2