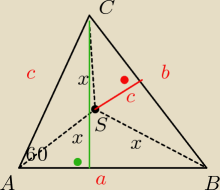
w dobrą stronę idę TOmek: Suma długości boków AB i AC trójkąta o polu 40√3 jest równa 26. kąt BAC ma miare 60^o. Oblicz odległość od boku BC punktu, który jest jednakowo odległy o wszystkich wierzchołkow tego trójkąta. Ja to tak zrobiłem: |AB| + |AC|=26 a+c=26 a=26−c c=26−a

	h
sin60o=
	c

	a*h
40√3=
	2

c= 26−a, więc

	h
sin60o=
	26−a

	a*h
40√3=
	2

układ równań, w dobrą stronę idę

TOmek:

jeden taki: ja bym to zrobił tak: układ: P=1/2 * ac*sin60 a+c=40√3 wyznaczas a i c potem z twierdzenia cosinusów b a potem z twierdzenia sinusów

	b
2R=
	sin60

R to u Ciebie x

jeden taki: ale to nie iksa nie szukamy heheh

jeden taki: oczywiście pogubiłem się i zamieszałem a+c=26 powodzenia

Godzio: z tw. cos i sin dojdzie się do tej samego wyniku b = √3R

Godzio: Zaraz rozpiszę to zadanie

Godzio:

	1
P =		a * c * sin60o = 40√3 ⇒ ac = 160
	2

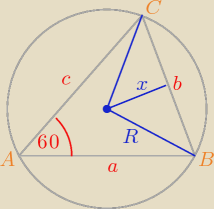
a + c = 26 Z twierdzenia sinusów dla ABC:

b
	= 2R
sin60o

b = √3R

	b√3
Z Pitagorasa policzysz że x =
	6

Z twierdzenia cosinusów dla ABC mamy: b² = a² + c² − 2ac * sin60^o = (a + c)² − 2ac − √3ac = (a + c)² − ac(2 + √3) b = ... x = ...

Godzio: jeden taki jednak dobrze mówiłeś mi się coś ubzdurało że chodziło o trójkąt SBC

TOmek: Dziekuje, ale mi głownie chodzi czy moje obliczenia są dobre Bo z nich takze dojdę do wyniku