Stereometria - przekroje wielościanów michal: Ostrosłup prawidłowy czworokątny ma krawędź podstawy długości 6cm i wysokość 4 cm. Płaszczyzna P przechodzi przez jedną z krawędzi jego podstawy i jest prostopadła do przeciwległej ściany bocznej. Narysuj przekrój ostrosłupa tą płaszczyzną i oblicz pole tego przekroju. Narysować umiem. Nie wiem za to co mam zrobić z informacją: "jest prostopadła do przeciwległej ściany bocznej". Czy to znaczy, że dzieli ją na pół?

voltage: To znaczy, że jest prostopadła i nic więcej

michal: Rozumiem. Mimo to nie pomogło mi to w zadaniu, nie widzę żadnego zastosowania dla tej informacji.

voltage: Aktualnie myślę nad tym zadaniem, wyrysuj sobie przydatne szkice przekrojów, które będą mogły się przydać do rozwiązania.

voltage: Nie ja już nie wyrabiam, spróbuję jeszcze poźniej podejść do tego zadania, może w tym czasie ktoś inny Ci pomoże

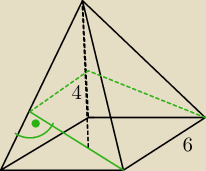
Grześ: Przekrojem tym jest trapez Mam już koncepcje tak zrobić to zadanie, chwilę to przemyslę. Trudny będzie opis, bo cięzko jest wyjaśnić powstające figury płaskie, w figurze przestrzennej

Grześ: Wewnątrz ostrosłupa powstanie nam trójkąt, o bokach 4,3 oraz przeciwprostokątnej x, która jest wysokością ściany bocznej. Jak prosto policzyć wynosi ona 5, ta wysokość ściany bocznej. Teraz mamy daną ścianę boczna o wymiarach 6 podstawa i 5 wysokość. Liczymy ramię ściany bocznej: d=√3³+5³=√34 Mamy długość ściany bocznej, zaraz przedstawię dalszy krok obliczeń

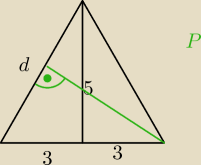
Grześ: Musimy obliczyć wysokość zielona ściany bocznej, która w naszym przekroju jest ramieniem trapezu Pole trójkąta wyraża się na dwa sposoby:

	1
P=		6*5
	2

oraz

	1
P=		√34*hx
	2

Porównujemy je:

1		1
	6*5=		√34*hx
2		2

	30
hx=
	√34

	30
Mamy już daną podstawę dolną 6, oraz dwa ramienia trapezu
	√34

Zaraz cią dalszy obliczeń, chwilka zastanowienia

Grześ: I w tym momencie utknąłem, myślcie, bo nie mogę wykombinować jak policzyć podstawę górną przekroju, lub wysokość jego

voltage: To utknąłeś tam gdzie ja haha

Grześ: Już wiem, kontynuuje obliczenia

voltage: Oooo!

voltage: Czyżby z podobieństwa?

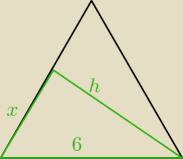
Grześ: Korzystam nadal z rysunku z poprzedniego postu, liczę z Pitagorasa:

900
	+x2=62
34

	324
x2=
	34

	18
x=
	√34

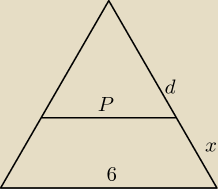
Grześ: Teraz wystarczy z podobieństwa wyznaczyć: d=√34

	18
x=
	√34

P		6
	=
d−x		d

	6(d−x)
P=
	d

	18   6(√34− )   √34
P=
	√34

	18		16		96
P=6(1−		=6*		=
	34		34		34

Mamy górną podstawę

Grześ: Teraz tylko wyliczyć wysokość tego trapezu Chcesz to voltage zrobić

voltage: Powiem Ci że tak średnio, aczkolwiek moge spróbować

Grześ: Masz dane wszystko, podstawę dolną, podstawę górną i ramiona trapezu, teraz utwórz jakiś trójkąt prostokątny i liczymy

voltage: No już widzę

Grześ: masz to voltage

voltage: Podam wynik

voltage:

	110736
h=√
	4624

Nie wiem, może udało dojść Ci się do ładniejszej postaci

voltage: Bardziej uproszczone

	6921
h=√		Może da się dalej, ale ja już naprawdę nie mam siły
	289

voltage: h≈√23,95

voltage: Czy potwierdzasz ten wynik?