W okrąg o promieniu r wpisano prostokąt, a następnie środki kolejnych boków połą Ater: W okrąg o promieniu r wpisano prostokąt, a następnie środki kolejnych boków połączono odcinkami. Jaki czworokąt otrzymano? Wykaż,że obwód tego czworokąta jest równy 4r.

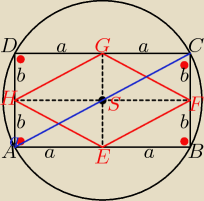
Basia: jakie są trójkąty EAH,EBF,GCF GDH i co z tego wynika ? jakie są odcinki AS i HE i co z tego wynika ?

Ater: otrzymany czworakat jest rombem

Basia: owszem, a wiesz dlaczego ?

Ater: jego przekątne (czyli długości boków prostokąta) przecinają się pod kątem prostym, a każdy bok rombu jest równy długości połowy przekątnej prostokąta, dobrze mysle?

Ater: juz wiem o co chodzi dziękuje Ci Basiu za podpowiedź

Basia: dobrze myślisz można też tak trójkąty: ESF, FSG, GSH i HSA są prostokątne i mają jednakowe przyprostokątne ⇒ są przystające ⇒ EF = FG = GH = HA i EF||AC||GH i FG||BD||HA ⇒ EFGH jest rombem EF=FG=GH=HA = ¹₂AC = ¹₂*2r = r Ob = 4r