zad
maciej: zna sie ktos na krzywych stozkowych?
13 lis 13:14
Basia:
na których ?
13 lis 13:16
maciej: hiperboli paraboli elipsy

13 lis 13:18
Basia:
mniej więcej, wzorów już nie pamiętam na kierownicę i mimośród na przykład, ale to można
znaleźć
13 lis 13:20
maciej: mimosrod e=c/a
kierownica tez nei wiem
13 lis 13:23
maciej: skad wiadomo co to jest x2−2x+2y2+4y−8=0?
13 lis 13:24
Basia:
x
2−2x = (x−1)
2−1
2y
2+4y = 2(y
2+2y) = 2[(y+1)
2−1]
stąd
x
2−2x+2y
2+4y−8=0
(x−1)
2−1+2[(y+1)
2−1]−8=0
(x−1)
2+2(y+1)
2=11 /:11
a to jest równanie elipsy
środek S(1,−1)
a
2=11 ⇒ a=
√11 ⇒ oś pozioma 2a=2
√11
| | √11 | | √22 | |
b2=112 ⇒ b= |
| = |
| ⇒ oś pionowa 2b= √22 |
| | √2 | | 2 | |
13 lis 13:31
maciej: oka np mozna rozpoznac hiperbole po tym ze wspolczynniki przy y2 i x2 sa roznych znakow tak?
13 lis 13:34
brg: A ja mam zadanie z krzywych stożkowych :
wyznaczyć równanie paraboli której :
kierownicą jest prosta o równaniu: y=x−7 a wierzchołkiem punkt F: (3,1).
13 lis 13:35
Basia:
tak
13 lis 13:35
maciej: a mozesz naisac jakies rownanie parabolii je rozwiazac bo za abdz nie rozumiem wzoru
(y−yo)2=2p(x−x0)
13 lis 13:36
maciej: lub w centralnym y2=2px
13 lis 13:37
Basia:
trzeba przypomnieć wzory
ale nie podoba mi się równanie kierownicy
na pewno dobrze przepisałeś ?
to jest do zrobienia, z kierownicą y=x−7, ale będzie drańsko skomplikowane
13 lis 13:38
maciej: to nei bedzie y2=12x−7?
13 lis 13:40
maciej: a wogole mozesz podac jakies przyklad o danej kierownicy i ognisku ? w polozeniu centarnym i
oglnym na prostych przykladach jak to si eliczy?
13 lis 13:40
Basia:
w tym rzecz, że te wzory dotyczą paraboli której oś symetrii jest równoległa do osi OX
wtedy kierownica jest prostopadła do OX
a prosta y=x−7 nie jest prostopadła do OX
trzeba by było obracać układ współrzędnych, a to już się bardzo komplikuje
13 lis 13:41
maciej: a moze byc np podana kierownica i wzor i obliczyc ognisko albo podane ogniako i wzor paraboli i
obliczyc kierownice? podajcie jakies przyklady

13 lis 13:41
Basia:
no wprawdzie tylko o 45 stopni, ale i tak będzie wredne
13 lis 13:42
Basia:
y2=4x
y2=2px
2p=4
p=2
kierownica x=−p2 x=−1
ognisko P(1,0)
(y−1)2=16(x−2)
wierzchołek S(2,1)
kierownica x=−8
ognisko P(8,0)
13 lis 13:46
brg: rówanie kierownicy jest na 100% ok.
a co do przykladu, to mam kiepskie notatki z wykładu..
w sumie mozna uzyć wzoru dla ogniska o współrzędnych (0, p)
i kierownicy y=−p tj. y=1/4p *x2
13 lis 13:47
Basia:
w tym drugim:
kierownica: x=−6
ognisko: P(10,0)
13 lis 13:48
brg: i tak jak basia wspomniala ten wzor jest praktycznie bezużyteczny

13 lis 13:48
Basia:
nie można, bo w Twoim przykładzie kierownica nie ma równania postaci y=−p
13 lis 13:49
maciej: a dla kogo to?
y2=4x
y2=2px
2p=4
p=2
kierownica x=−p2 x=−1
ognisko P(1,0)
(y−1)2=16(x−2)
wierzchołek S(2,1)
kierownica x=−8
ognisko P(8,0)
13 lis 13:51
brg: wiem , dlatego pytałem czy ktos umie rozwiazac przykład z kierwonicą y=x−7 ^^
13 lis 13:52
Basia:
trzeba obrócić układ współrzędnych o 45 stopni
policzyć w tym nowym i dopiero potem wrócić do starego
maciej
nie kierownica paraboli
y2=12x−7 = 12(x−712) ma równanie
x=−6+712
13 lis 13:53
maciej: (y−1)2=16(x−2)
wierzchołek S(2,1)
kierownica x=−8
ognisko P(8,0)
w tym przypadku kierownica nie bedzie x=xo−p/2 czyli x=−1−4=−3?
13 lis 13:56
maciej: −5 sory
13 lis 13:56
maciej: aj 1+−4 czyli −3 dobrze

13 lis 13:58
maciej: i ognisko 1+4=5 czyli F=(5,0)?
13 lis 13:58
Basia:
jest też inny sposób, dla mnie prostszy, bo wzorów na obrót układu nie trzeba szukać, ale nie
wiem czy zadowoli prowadzącego zajęcia.
parabola to zbiór punktów równo odległych od kierownicy i ogniska
1. piszę równanie prostopadłej do k: y=x−7 i przechodzącej przez F(3,1)
to oś symetrii paraboli l:
2. szukam punktu A wspólnego k: i l:
3. wyznaczam P taki AF→=FP→ to będzie ognisko
4. szukam punktów równo odległych od k: i od P
13 lis 14:01
Basia:
maciej
tak, jeżeli wierzchołek nie jest w (0,0) to kierownica i ognisko też są przesunięte
pisałam poprawkę do tego, ale ją "wcięło"
13 lis 14:04
Basia:
2p=16
p=8
x0=2
x=x0−p2=2−4= −2
P(x0+p2,0) = (6,0)
13 lis 14:06
maciej: dzikei

13 lis 14:09
maciej: mozna po ognisku i kierownicy poznacw jakim polozeniu jest parabola czy musi to pisac?
13 lis 14:10
Basia:
można poznać
oś symetrii paraboli jest prostopadła do kierownicy przechodząca przez ognisko
wierzchołek to środek odcinka od punktu przecięcia kierownicy z osią symetrii do ogniska
13 lis 14:26
maciej: przyklad

?
13 lis 14:32
Basia:
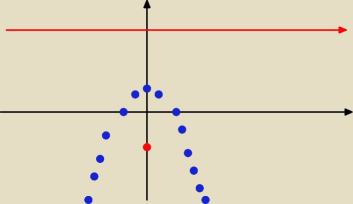
13 lis 14:34
maciej: polozenie ogolne tak?
13 lis 14:35
Basia:
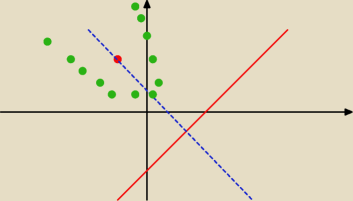
ale tylko mniej więcej; bo już jak dokładnie ramiona się rozchodzą nie wiadomo
13 lis 14:37
maciej: to jakie wymiary musi miec keirownica i ognisko w polozeniu centralnym a jakie w polozeniu
ogolnym
dobrze mysle ze w polozeniu centralnym ognisko bedzie (liczba,0) a wpolozeniu
ogolnym(liczba,liczba)? sory za takie pyt ale nie bylo mnei na wykladzie
13 lis 14:53
maciej:
13 lis 15:18
maciej:
13 lis 16:09
Basia:
w położeniu centralnym może być (liczba,0) (pozioma oś symetrii) lub (0,liczba) (pionowa oś
symetrii)
w ogólnym zgadza się (liczba, liczba)
13 lis 16:19
maciej: a po kierownnicy samej da rady poznac?
13 lis 16:33
Basia:
nie
13 lis 16:48





 ?
?

 ale tylko mniej więcej; bo już jak dokładnie ramiona się rozchodzą nie wiadomo
ale tylko mniej więcej; bo już jak dokładnie ramiona się rozchodzą nie wiadomo