Kat rozwarcia stozka jest rowny 78 stopni a jego wysokosc wynosi 12 cm.Oblicz pr
magda: Kat rozwarcia stozka jest rowny 78 stopni a jego wysokosc wynosi 12 cm.Oblicz promien podstawy
i tworzaca stozka (z dokladnoscia do 1 mm)
13 lis 12:45
dero2005:
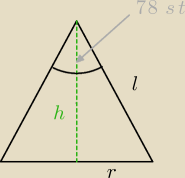
Dane: h− wysokość stożka = 12 cm = 120 mm
α − kąt rozwarcia 78°
Z rysunku
rh = tg
α2 = tg 39°
tg 39° = 0,8097 z tablic
promień r= h* 0,8097 = 12 * 0,8097 = 9,71 cm = 97 mm
tworząca l =
√r2+h2 = 154,3 mm = 154 mm ponieważ 3<5
13 lis 14:03
g1en1us1a: Oblicz wysokość stożka którego tworząca ma długość 17cm a podstawą jest koło o polu 200,96 cm
kwadratowych. W obliczeniach przyjmij π=3,14.
17 wrz 20:28
dero2005:
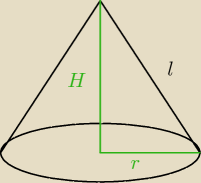
l = 17 cm
P
p = 200,96 cm
2
P
p = πr
2 = 200,96
r =
√64 = 8 cm
H =
√l2 − r2 =
√172 − 82 =
√289−64 =
√225 = 15 cm
17 wrz 21:39
g1en1us1a: Dziękuję
18 wrz 18:42
Agnieszka:
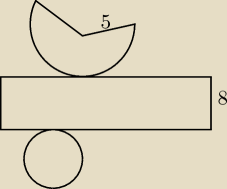
Rysunek przedstawia siatkę bryły o polu powierzchni całkowitej 72π. Oblicz objętość tej bryły.
18 wrz 18:52
g1en1us1a: 9.21.
Objętość stożka o promieniu podstawy 3 jest równa 6π. Wyznacz sinusa kąta nachylenia tworzącej
stożka do płaszczyzny podstawy.
9.24.
Powierzchnia boczna stożka po rozwinięciu jest wycinkiem koła o kącie 120 stopni i promieniu
27cm. Oblicz pole podstawy tego stożka.
9.26.
Z koła o promieniu 8 wycięto wycinek o kącie 45 stopni. Z reszty koła wykonano powierzchnię
boczną stożka. Oblicz objętość tego stożka.
18 wrz 19:20
dero2005:
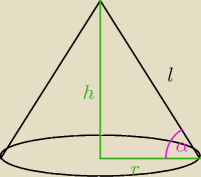
r = 3
h = 2
l =
√h2 + r2 =
√22 + 32 =
√13
| | h | | 2 | | 2√13 | |
sinα = |
| = |
| = |
| |
| | l | | √13 | | 13 | |
18 wrz 19:38
dero2005:
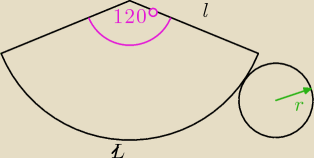
l = 27
r = 9
P
p = πr
2 = 81π cm
2
18 wrz 19:51
dero2005:
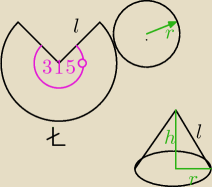
l = 8 cm
r = 7 cm
h =
√l2 − r2 =
√82 − 72 =
√15
| | πr2*h | | π72*√15 | | 49 | |
V = |
| = |
| = |
| π√15 |
| | 3 | | 3 | | 3 | |
18 wrz 20:08
g1en1us1a: Dziękuję z całego serca. Miło mi, że jest ktoś, kto chce pomóc.
18 wrz 20:55
g1en1us1a: (zadanie maturalne)
Objętość walca i stożka są równe. Promień podstawy stożka jest dwa razy większy od promienia
podstawy walca, a wysokość stożka jest o 1 mniejsza od wysokości walca. Oblicz stosunek pola
powierzchni stożka do pola powierzchni walca, jeżeli tangens kąta między tworzącą stożka, a
jego wysokością jest równy 3/4. (trzy czwarte).
Prosiła bym o dokładne obliczenia i możliwe wytłumaczenie skąd jakie liczby wychodzą, ponieważ
nie zrozumiałe jest dla mnie to zadanie. Z góry, dziękuję.
21 wrz 22:07
dero2005:
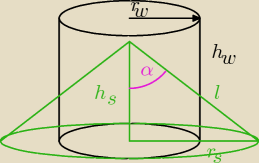
Oznaczenia:
r
s promień stożka
h
s wysokość stożka
l tworząca stożka
α kąt między tworzącą stożka a wysokością
r
w promień walca
h
w wysokość walca
Warunki zadania:
V
w = V
s
r
s = 2r
w
h
s + 1 = h
w
Obliczyć:
V
w = πr
w2*h
w
r
s2*h
s = 3r
w2*h
w
podstawiamy h
s = h
w−1 , r
s = 2r
w
(2r
w)
2*(h
w−1) = 3r
w2*h
w
4r
w2(h
w − 1) = 3r
w2*h
w |: r
w2
4(h
w − 1) = 3h
w
4h
w − 4 = 3h
w
4h
w − 3h
w = 4
hw = 4
−−−−−−−−−−−−−−−
h
s = h
w − 1 = 4 − 1 = 3
hs = 3
rs = 94
rw = 98
z Pitagorasa
l
2 = r
s2 + h
s2
| | 15 | |
l = √rs2 + hs2 = √(94)2+32 = |
|
|
| | 4 | |
l = 154
P
cs = πr
s2 + πr
sl = πr
s(r
s+l)
P
cw = 2πr
w2 + 2πr
w*h
w = 2πr
w(r
w+h
w)
22 wrz 00:02
g1en1us1a: Prosiłabym o dokładne objaśnienia, jak w zadaniu poprzednim.
1. Kartka papieru o wymiarach 20cm x 30cm można zwinąć tak, by utworzyć z niej powierzchnię
boczną walca. Jaką objętość będzie miał taki walec? Rozważ 2 przypadki.
2. Dwie metalowe kule o promieniach 1cm i 2cm przetopiona na jedną kulę. Oblicz jej pole
powierzchni całkowitej.
3. Po zwinięciu wycinka kołowego o promieniach 8 i kącie środkowym 270 stopni otrzymano
powierzchnię boczną pewnego stożka. Oblicz objętość tego stożka.
4. Przekrój osiowy stożka jest trójkątem równobocznym o polu 18. Oblicz pole powierzchni
bocznej stożka.
5. Promieć podstawy stożka o objętości 72π jest trzy razy krótszy niż tworząca.
a) wyznacz tanges kąta nachylenia tworzącej stożka do jego podstawy
b) oblicz pole powierzchni całkowitej stożka.
24 wrz 13:29
dero2005:
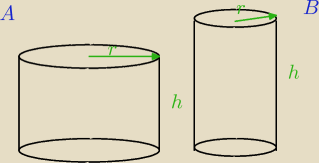
Przypadek A
h = 20
2πr = 30
| | 4500 | |
V = πr2*h = π*(15π)2*20 = |
|
|
| | π | |
Przypadek B
h = 30
2πr = 20
| | 3000 | |
V = πr2*h = π(10π)2*30 = |
| |
| | π | |
29 wrz 21:35
dero2005:
zad 2
liczymy objętości tych kul
| | 4 | | 4 | | 4 | |
V1 = |
| πr3 = |
| π*13 = |
| π cm3
|
| | 3 | | 3 | | 3 | |
| | 4 | | 32 | |
V2 = |
| π*23 = |
| π cm3
|
| | 3 | | 3 | |
dodajemy objętość kul
| | 4 | | 32 | |
V = V1 + V2 = π( |
| + |
| ) = 12π
|
| | 3 | | 3 | |
teraz liczymy promień kuli dużej (zsumowanej)
r =
3√9
liczymy powierzchnię dużej kuli
S = 4πr
2 = 4*π*(
3√9)
2 = 4π
3√81 cm
2
29 wrz 21:50
dero2005:
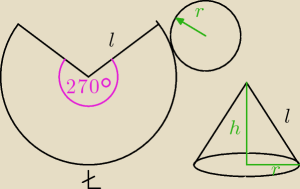
zad 3
l = 8
liczymy długość łuku wycinka kołowego (jest ona równa długości obwodu podstawy)
r = 6 → promień podstawy
mamy promień podstawy r, tworzącą l, liczymy wysokość h z pitagorasa
h =
√l2 − r2 =
√82 − 62 =
√28 = 2
√7 cm
teraz liczymy objętość
| | πr2*h | | π*62*2√7 | |
V = |
| = |
| = 24π√7 cm3 |
| | 3 | | 3 | |
29 wrz 22:07
dero2005:
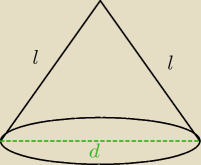
zad 4
przekrój osiowy jest trójkątem równoboczym czyli d = l = 2r
wzór na pole trójkata równobocznego wygląda tak
gdzie a = d = l = 2r = 2
√2*
4√27
stąd r =
√24√27
wzór na pole powierzchni bocznej stożka wygląda tak
P
b = πrl podstaw dane do wzoru i oblicz
29 wrz 22:32
dero2005:
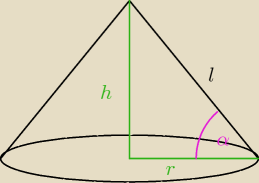
zad 5
l = 3r
r
2*h = 216
z pitagorasa
l
2 = r
2 + h
2
wstawiamy do pierwszego wzoru
h = 12
r =
√18 = 3
√2
liczymy tg kąta α nachylenia tworzącej do podstawy
| | h | | 12 | |
tg α = |
| = |
| = 2√2
|
| | r | | 3√2 | |
P
c = πr(r+l) = podstaw dane i policz
29 wrz 22:51
g1en1us1a: Witaj, mam parę zadań do obliczenia. Niestety za każdym razem wychodzą mi inne wyniki, niż
widniejące w karcie odpowiedzi. Proszę, jeśli byłoby to możliwe, obliczenia pisać dość
wyrozumiale następujących przykładów. Z góry bardzo dziękuję.
1. Narysuj w układzie współrzędnych prostą daną w postaci kierunkowej i napisz jej równanie w
postaci ogólnej.
a) y=2x− 3
b) y= − 1/2x (minus jedna druga) −1
c) y=2/3x +2
d) y= −2
e) y= −3x+1
f) y= 1/4x −2
2. Dane równanie prostej zapisz w postaci kierunkowej.
a) 2x−5y+15=0
b)2x−3y−6=0
c) √3x+3y−1=0
d) 3√2x+6y−1=0
3. Wyznacz równanie prostej przechodzącej przez punkty A i B.
a) A=(−2, −3), B=(5,−3)
b) A=(−1, 4), B=(2, −2)
c) A=(2, −1), B=(2, 3)
d) A=(−3, −5), B=(2, 4)
4. Sprawdź, czy punkty A, B, C są współliniowe.
a) A=(1, 2), B=(0, −1) C=(−1, −4)
b) A=(−1, 5), B=(2, 2) C=(93, 1)
c) A=(0, 0), B=(1, −3), C=(2, −5)
5. Napisz równania prostych zawierających boki trójkąta o wierzchołkach A, B, C.
a) A=(−3, −3), B=(3, −1), C=(1, 5)
b) A=(−2, 2), B=(0, 5), C=(−2, 11)
6. Wyznacz równanie prostej równoległej do prostej k i przechodzącej przez punkt P.
a) k : y = 2x−1, P=(3, 2)
b) k : 2x−y+5=0, P=(−1, 1)
c) k : 2x+3=0, P=(2, 5)
d) k : y −√7=0, P=(3, 0)
7. Wyznacz równanie prostej prostopadłej do prostej l i przechodzącej przez punkt P.
a) l : y =3x, P=(0, 2)
b) l : y = −1/2x −1, P=(3, 1)
c) l : x −5y+2=0, P=(−1, 2)
d) l : y = −5, P=(3, 7)
29 lis 17:49
tomek: Objetość stożka jest równe 375cm sześciennych. A pole 75cm kwadratowych. Oblicz promien i
wysokość stożka
4 gru 09:58
 Dane: h− wysokość stożka = 12 cm = 120 mm
α − kąt rozwarcia 78°
Z rysunku rh = tgα2 = tg 39°
tg 39° = 0,8097 z tablic
promień r= h* 0,8097 = 12 * 0,8097 = 9,71 cm = 97 mm
tworząca l = √r2+h2 = 154,3 mm = 154 mm ponieważ 3<5
Dane: h− wysokość stożka = 12 cm = 120 mm
α − kąt rozwarcia 78°
Z rysunku rh = tgα2 = tg 39°
tg 39° = 0,8097 z tablic
promień r= h* 0,8097 = 12 * 0,8097 = 9,71 cm = 97 mm
tworząca l = √r2+h2 = 154,3 mm = 154 mm ponieważ 3<5
 l = 17 cm
Pp = 200,96 cm2
Pp = πr2 = 200,96
l = 17 cm
Pp = 200,96 cm2
Pp = πr2 = 200,96
 Rysunek przedstawia siatkę bryły o polu powierzchni całkowitej 72π. Oblicz objętość tej bryły.
Rysunek przedstawia siatkę bryły o polu powierzchni całkowitej 72π. Oblicz objętość tej bryły.
 r = 3
r = 3
 l = 27
l = 27
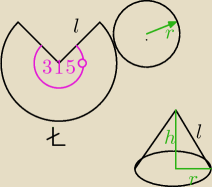 l = 8 cm
l = 8 cm
 Oznaczenia:
rs promień stożka
hs wysokość stożka
l tworząca stożka
α kąt między tworzącą stożka a wysokością
rw promień walca
hw wysokość walca
Warunki zadania:
Vw = Vs
rs = 2rw
hs + 1 = hw
Oznaczenia:
rs promień stożka
hs wysokość stożka
l tworząca stożka
α kąt między tworzącą stożka a wysokością
rw promień walca
hw wysokość walca
Warunki zadania:
Vw = Vs
rs = 2rw
hs + 1 = hw
 Przypadek A
h = 20
2πr = 30
Przypadek A
h = 20
2πr = 30
 zad 3
l = 8
liczymy długość łuku wycinka kołowego (jest ona równa długości obwodu podstawy)
zad 3
l = 8
liczymy długość łuku wycinka kołowego (jest ona równa długości obwodu podstawy)
 zad 4
przekrój osiowy jest trójkątem równoboczym czyli d = l = 2r
wzór na pole trójkata równobocznego wygląda tak
zad 4
przekrój osiowy jest trójkątem równoboczym czyli d = l = 2r
wzór na pole trójkata równobocznego wygląda tak
 zad 5
l = 3r
zad 5
l = 3r