wartość bezwględna aa: |x−3|+2=3x+3

Marcin W: |x−3|=3x+5 D: 3x+5≥0 3x+5=x−3 lub 3x+5=−x+3 2x=−8 4x=−2 x=−4 (odpada) x=−0,5

M4ciek: Wydaje mi sie , ze Df: 3x + 5 > 0 , a nie 3x + 5 ≥ 0 Bo dla Ix−3I = 0 mamy jedno rozwiazanie A tak w ogole to trzeba wyznaczac dziedzine? Uwazam , ze tak jest poprawnie : 1^o dla x∊(−∞,3) −x+3+2=3x+3 −4x=−2

	1
x=		∊ (−∞,3)
	2

2^o dla x∊<3,+∞) x−3+2=3x+5 −2x=6 x=−3 ∉ <3,+∞)

	1
Odp.Koncowa x=
	2

Marcin W: tak wogole to sie pomylilem powinno byc |x−3|=3x+1 i wtedy dziedzina 3x+1≥0 bo przeciez wartosc bezwgledna moze byc rowna zero

Marcin W: ma byc ≥ napewno w dziedzinie no i co z tego M4aciek ze |x−3|=0 ma jedno rozwiazanie ale ma

M4ciek: Ok ok ,ale to nie zmienia faktu bo wg mnie w ogole nie trzeba jej wyznaczac bo to jest oczywiste ze : IaI ≥ 0 bo wynika to z wartosci bezwzglednej,a i tak trzeba rozbic na przypadki.

Marcin W: x−3=3x+1 2x=−4 x=−0,5 odrzucam wlasnie przez dziedzine lub x−3=−3x−1 4x=2 x=0,5

Marcin W: ale u mnie jest rozbite na dwa przypadki po drugie trzeba wyznaczyc dziedzine bo inaczej wyjda dwa rozwiązania 0,5 oraz −0,5 w moim sposobie (wiec jest to tu istotne) Pozdrawiam

M4ciek: Oba sposoby sa dobre bo ja likwiduje moja jedna odpowiedz przez to ,ze nie nalezy do danego przedzialu Tylko rozpisalem ,zeby bylo czytelniej

Marcin W: wiec nie ma co wypisywac

M4ciek: Ja to dla siebie tez robie matura za pasem

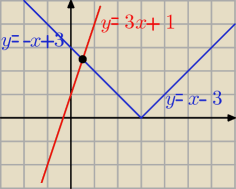
Bogdan: Można i tak rozwiązać:

	1		1		1
−x + 3 = 3x + 1 ⇒ 4x = 2 ⇒ x =		, y = −		+ 3 = 2
	2		2		2