Zmaleźć wyrazy ciągu liczbowego. qam: Witam. Mógłby ktoś mi pomóc z tymi zadaniami: 1.Oblicz, ile wyrazów ciągu a_n jest większych od −10, a mniejszych od 50. Wyznacz te wyrazy: a) a_n=24n−94 b) a_n=n²−2n−30 3.Dany jest ciąg określony wzorem: a_n=n²−7n−8 a) Oblicz, ile wyrazów ciągu należy do przedziału <50,100> Z góry dziękuję za pomoc.

sushi_ gg6397228: 1 trzeba rozwiazac nierownosci a) −10< 24n−94 24n−90 <50 zad 3 tak samojak pierwsze

qam: Właśnie tak zrobiłem, ale otrzymuję wyniki zupełnie inne niż książkowe odpowiedzi.

sushi_ gg6397228: liczby trzeba potem zaokraglic do gory lub dołu

qam: Zaokrąglałem, ale i tak jest źle. Możesz napisać swoje rozwiązanie?

nikka: Zad. 1 a) −10 < 24n −94 < 50 84 < 24 n < 144

84		144
	< n <
24		24

7
	< n < 6
2

	1
3		< n < 6 i n∊N
	2

n = { 4, 5} czyli dwa wyrazy Spr. a₃ = 72−94 = −22 < −10 a₄ = 2 a₅ = 24 a₆ = 50 Faktycznie będą to tylko dwa wyrazy.

sushi_ gg6397228: ja wiem ile bedzie, zapisz swoje obliczenia

qam: 1a) zrobiłem tak jak @nikka, w odp jest a₆,a₇,a₈,a₉ 1b) wyszło mi a₅,a₆,a₇,a₈,a₉, w odp jest a₄,a₅ 3a) mam a₁1,a₁2,a₁3,a₁4, w odp jest, że 11 początkowych wyrazów ciągu.

qam: Przepraszam pomyłka 3a) mam a₁₁,a₁₂,a₁₃,a₁₄, w odp jest, że 11 początkowych wyrazów ciągu.

sushi_ gg6397228: 1a) wyniki z ksiazki sa błedne lub źle podalas pierwszy przyklad 1b) pokaz obliczenia, a nie suche liczby 3 a₁= 1−7−8= −14 nie nalezy do przedzialu moze odpowiedz masz nie do tych zadan −−> wiec pokaz swoje obliczenia

qam: 1b) n²−2n−30>−10 |(−1) −n²+2n+30<10 −n²+2n+20<0 Δ=48 √Δ=√48 czyli: x₁≈4,46 x₂≈−2,46 n∊(−∞; −2,46> + <4,46;+∞) n²−2n−30<50 n²−2n−80<0 Δ=324 √Δ=18 czyli: x₁=−8 x₂=10 n∊<−8,10> zbiór rozwiązań obu nierówności: n∊<−8;−2,46>+<4,46;10> a więc 6 wyrazów n₅,n₆,n₇,n₈,n₉,n₁₀

sushi_ gg6397228: powiedz , kto kazal mnozyc przez "minus1" n²−2n−30>−10 n² −2n−20>0 Δ= 4+4*1*20=...

sushi_ gg6397228: jak mamy problem z delta itp to robimy a₁= (1)²−2*(1)−30= ... a₂=... a₃=... a₄=.. a₅=... i liczymy na piechote

qam: Ale chyba mnożenie przez (−1) i tak nie zmieniło w tym wypadku wyniku?

qam: Ogólnie dobrze to zrobiłem czy nie?

sushi_ gg6397228: a po co "minus" przy najwyzszej potedze jeszcze źle policzylas delte

sushi_ gg6397228: tak dlugo liczysz jeszcze raz tą Δ

qam: Policzyłem od początku, ale i tak wyszło w 1b) a₆,a₇,a₈,a₉, więc z odp się nie zgadza. Już sam nie wiem co jest źle.

qam: Możesz napiszesz własne obliczenia, byłbym bardzo wdzięczny. Aha, mam jeszcze coś takiego, oczywiście znów nie zgadzają się wyniki: 6.Dany jest ciąg: a_n=−¹₂n²+8n−24 a)Ile wyrazów dodatnich ma ten ciąg? b)Które wyrazy tego ciągu są mniejsze od 4?

sushi_ gg6397228: 1b) a₆, a₇, a₈, a₉ dla a₁₀= 100−50=50 nie pasuje

sushi_ gg6397228: teraz czekam na obliczenia do zadania 3. oraz do zad6. 6a) a_n >0 podac "n" oraz tez z nazwiska, ktore to 6b) a_n <4 i podac z nazwiska, ktore to

patrycja: 5:23=

patrycja: 12≈4

patrycja: 456≈145

qam: Zad.3 d) 50≤n²−7n−8≤100 50≤n²−7n−8 0≤n²−7n−58 Δ=281 √Δ=√281 x₁=−4,88 x₂=11,88 czyli n∊<−4,88;11.88> n²−7n−8≤100 n²−7n−108≤0 Δ=481 √Δ=√481 x₁=−7,46 x₂=14,46 czyli n∊<−7,46;14,46> Zbiór rozwiązań obu nierówności: n∊<−7,46;−4,88> + <11,88;14.46> a więc 3 wyrazy a₁₂,a₁₃,a₁₄

sushi_ gg6397228: masz n² −7n−58>0 wiec masz ramiona do gory, a Ty liczysz dla mniejszego od 0

sushi_ gg6397228: n ∊(−∞; −4,88) ∪(11,88; +∞) ale wynik poprawny a₁₂, a₁₃, a₁₄

qam: Możesz to jakoś wyjaśnić, bo nie za bardzo rozumiem?

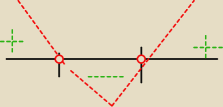
sushi_ gg6397228: 0< n² −7n−58 parabola do góry i jest dodadnia wartosc , wwiec jakim cudem robisz dla ujemnej

qam: 6a) −¹₂n²+8n−24>0 Δ=16 √Δ=4 x₁=12 x₂=4 n∊<4,12> więc są to wyrazy a₅,a₆,a₇,a₈,a₉,a₁₀,a₁₁ 6b) −¹₂n²+8n−24<4 −¹₂n²+8n−28<0 Δ=8 x₁≈5,17 x₂≈10,83 n∊(5,17;10,83) czyli są to wyrazy a₆,a₇,a₈,a₉,a₁₀ poprawnie?

Basia: poprawnie

qam: heh, oczywiście w odp jest inaczej 6a) od a₁ do a₇ (włącznie) 6b) wyrazy od a₁ do a₅ oraz wszystkie począwszy od a₁₁

qam: Dzięki wielkie za pomoc.