Wyznacz równanie okręgu o środku S=(1,1), odcinającego na prostej ... xyz: Wyznacz równanie okręgu o środku S=(1,1), odcinającego na prostej 3x−4y+31=0 cięciwę o długości 16.

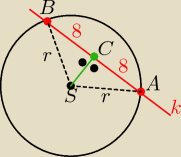
Eta: k: 3x −4y +31=0 S(1,1) liczymy odległość S od prostej k

	|1*3−1*4+31|		30
ISCI= d=		=		= 6
	32+(−4)2		5

ΔSAB jest równoramienny z tw. Pitagorasa w ΔCBS wyznacz r² i napisz równanie tego okręgu o: ( x−x_S)² + ( y−y_S)²= r²