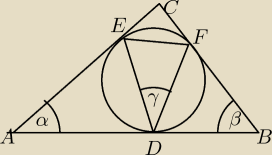
Udowodnij Problem: udowodnij, że γ=^α+β₂

zakłopotany: jak można to udowodnić?

Kuba: Trzeba do rysunku dorysować środek okręgu, oznaczyć go np. jako O i rozpatrywać czworokąt OECF. Gdy zauważymy, że ∡OEC=^π₂ i ∡OFC=^π₂ to natychmiast otrzymamy ∡EOF + ∡ECF = π. Ale ∡ECF=π−(α+β), więc ∡EOF=α+β. Z własności kąta środkowego i wpisanego na tym samym łuku γ=¹₂*∡EOF.

zakłopotany: a skąd wiadomo, że □OEC to ^π₂

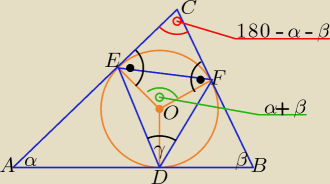
Bogdan: Suma miar kątów czworokąta EOFC jest równa 360^o Trzeba zastosować twierdzenie o kątach: wpisanym w okrąg i środkowym opartych na tym samym łuku. Kątem wpisanym jest kąt γ, kątem środkowym kąt EOF, którego miara jest równa α + β

zakłopotany: Dziękuję