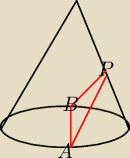
geometria Anuuula: Środek P tworzącej stożka połączono z końcami A i B średnicy koła w podstawie stożka tak, że AP=BP . Wiedząc, że kąt rozwarcia stożka jest równy 60 stopni , oblicz kąty trójkąta . błagam o wyjaśnienie lepsze niż na zadania info

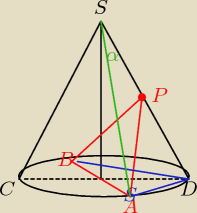
Basia: tr.CSD jest równoboczny ⇒ CD=CS=DS=2r ⇒PS=DS=r AP=BP ⇒AD=BD = a a²+a²=(2r)² 2a²=4r² a²=2r² a=r√2 w tr.ASD mamy ∡ASD=α AS=DS=2r AD=r√2 z tw.cosinusów AD²=AS²+DS²−2AS*AD*cosα 2r²=4r²+4r²−2*2r*2r*cosα 2r²=8r²(1−cosα) 1−cosα=¹₄ cosα=³₄ w tr.ASP mamy ∡ASP=α AS=2r PS=r z tw.cosinusów AP²=AS²+PS²−2*AS*PS*cosα AP²=4r²+r²−2*2r*r*³₄ AP²=5r²−3r² AP²=2r² AP=r√2 czyli tr.APB ma boki: AB=2r AP=BP=r√2 katy można wyliczyć z tw.cosinusów

Basia: to niebieskie S wzięło się nie wiadomo skąd; jest zbędne S w rachunkach to wierzchołek stożka czyli czarne S