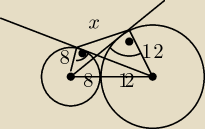
Oblicz x Pomocy!!!!: Oblicz x (koła są styczne zewn.)

Pomocy!!!!: jak mam rozwiązać ten przykład?

karo: Na powstałym czworokącie można opisać okrąg o średnicy 20. Jeżeli tak, to sumy przeciwległych boków są równe − sprawdź

Pomocy!!!!: sumy przeciwległych boków nie są równe

karo: Sorry, wróć. To nie sumy przeciwległych boków są równe, ale kątów. Skorzystaj z podobieństwa trójkątów

Pomocy!!!!: widzę już, które trójkąty są podobne, ale mam problem z użyciem odpowiedniego porównania, żeby obliczyć x

Pomocy!!!!: ale jak mam uwzględnić te podobieństwa trójkątów, mam za mało danych

Pomocy!!!!: mogę prosić Cię jeszcze o pomoc?

Pomocy!!!!: nie rozumiem

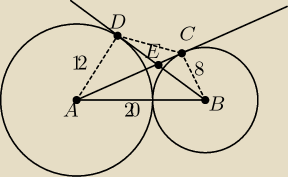
Kuba: Z góry przepraszam za rysunek − odwrotnie narysowałem okręgi − ale to bez znaczenia. Zadanie mnie męczy − jak ktoś ma proste rozwiązanie proszę o cynk. Ja rozumuję tak (ΔABC − trójkąt o wierzchołkach A,B i C, AB długość odcinka AB) : Oczywiste jest, że ΔAED i ΔBEC są podobne. Stąd mamy ^AE_EB=¹²₈ i ^DE_EC=¹²₈. CZyli 2*AE=3*EB i 2*DE=3*EC. Dzieląc stronami dostaniemy ^AE_DE=^EB_EC, czyli ΔAEB i ΔCED też są podobne, co juz oczywiste (przynajmniej dla mnie) nie było. Dokładając dwa równania z tw. Pitagorasa: 1) 12²+(DE+EB)²=20² 2) 8²+(AE+EC)²=20² do równań 3) 2*AE=3*EB 4) 2*DE=3*EC Mamy układ 4 równań z 4 niewiadomymi. I zaczynają się schody... Z równania 1) otrzymamy (DE+EB)²=256, stąd DE+EB=16 Z równania 2) podobnie (AE+EC)²=336, stąd AE+EC=4*√21 Z równania 3) AE=³₂*EB Z równania 4) DE=³₂*EC i po podstawieniu do 1) i 2) 1a) ³₂*EC+EB=16 2a) ³₂*EB+EC=4*√21 Z 1a) EB=16−³₂*EC i po podstawieniu do 2a) ³₂*(16−³₂*EC)+EC=4*√21 24−⁹₄*EC+EC=4*√21 ⁵₄*EC=24−4*√21 EC=^{96−16*√21}₅ EB=16−³₂*EC=16−^{288−48*√21}₁₀=^{48*√21−128}₁₀=^{24*√21−64}₅ Ale ^DC_AB=^EC_EB, więc szukany DC DC=20*^EC_EB Po żmudnych rachunkach (a pewnie się pomyliłem po drodze ) wyszło DC=^{16*√21−24}₅≈9.86 co wydaje sie wynikiem prawdopodobnym, aczkolwiek niekoniecznie właściwym ...