okrąg wpisany w czworokąt Milka: Na okręgu opisano trapez rónoramienny. Kąt rozwarty trapezu ma miarę 150, a odcinek łączący środki ramion ma 12 cm długości. Oblicz długość promienia okręgu. odp.r=3 cm

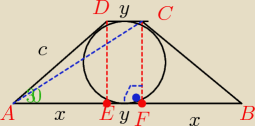
sushi_ gg6397228: |CF|=2r= |DE| mamy dane odcinek laczacy srodki ramion= 12 , wiec suma podstaw =24 1. 2x+2y= 24 ==> x+y= 12 trojkat AED

	x
2. cos30=
	c

trojkat ACD −tw cosinusow 3. |AC|²= c²+y² −2c*y* cos 150 |AC|²= c²+y² +2c*y* cos 30 −−> wstawaimy za cos 30 (kolor zielony) trojkat ACF Pitagoras 4. |AC|² = (x+y)² + |CF|² i kolejna zaleznosc trojkat ADE

	2r
5. tg 30=
	x

porownujemy 3 i 4

	x
c2+y2 +2c*y*		= (x+y)2 + |CF|2
	c

	x
c2+y2 +2c*y*		= (12)2 + (2r)2
	c

x+y=12

	2r
tg 30=
	x

	x
cos 30 =
	c

masz 4 zaleznosci

Milka: muszę chwilkę nad tym posiedzieć, wiedziałam, że to trudne jest

sushi_ gg6397228: ja sie zmywaj, wie sie mecz z tym

Milka: fajny jesteś

Milka: i taki mądry, szkoda że wcześniej nie wiedziałam o tej stronie

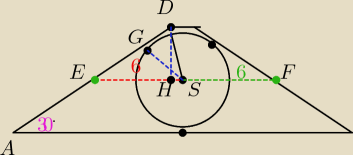
sushi_ gg6397228: jednak mozna inaczej to zobic kolor niebieski to jest promien (r) rozpatrzny trojkat ESD

	|ES|*|DH|		|ED|*|GS|
pole trojkata :		====		(SG to wysokosc trojkata)
	2		2

czyli (|DH|=|SG|= r) |ES|*|DH| ====|ED|*|GS| 6*r ====|ED|*r ==> |ED|= 6 zatem |AD|= 2* |DE|= 12 i teraz korzystamy z tej trygonometrii, co byla na poprzednim rysunku

	x		√3		x
cos 30=		==>		=		==> x= ...
	|AD|		2		12

	2r		√3		2r		x* √3
tg 30=		==>		=		===> 2r=
	x		3		x		3