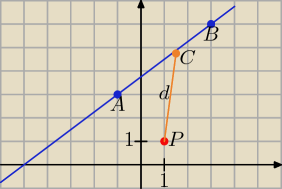
funkcja Aska: Proszę o pomoc bo to dla mnie czarna magia Dany jest odcinek AB, gdzie A=(−1;3), B=(3;6). Funkcja f przyporządkowuje dowolnemu punktowi należącemu do odcinka AB jego odległość od punktu P=(1;1). Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.

Bogdan:

	6 − 3		3
Prosta zawierająca punkty A(−1, 3), B(3, 6): y = ax + b, a =		=		.
	3 + 1		4

	3		3		3
y =		(x + 1) + 3 ⇒ y =		x + 3
	4		4		4

	3		15
Każdy punkt na tej prostej ma współrzędne (x, y) = (x,		x+		).
	4		4

Odległość d dowolnego punktu tej prostej od punktu P(1, 1) wyraża się zależnością: d = √ (x − 1)² + (y − 1)² = √ (x − 1)² + ( (3/4)x + (15/4) − 1)² Określamy funkcję opisaną w zadaniu: f(x) = √ (x − 1)² + ( (3/4)x + (11/4))² dla x∊<−1, 1>

Aska: a dlaczego w tylko zbiorze x∊<−1,1>?

Bogdan: Poprawiam, x∊<−1, 3>

Aska: dzięki jeszcze jedno pytanie jeśli się nie mylę, to najmniejszą wartością będzie odcinek PA? trzeba to jakoś udowadniać?