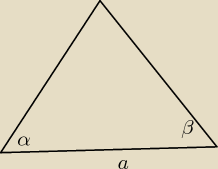
problem TOmek: Jeden z boków trójkąta ma długość a, zaś kąty trójkąta przległe do tego boku mają α i β. a)znajdź promień okręgu opisanego na tym trójkącie b)wyznacz długość pozostałych boków trójkąta c)znajdz promien okręgu wpisanego w ten trójkąt.

	a
a) 2R=		/:2
	sin(180−α+β)

	a
R=
	2 * sin(180−α+β)

dobrze zrobiłem a)

Jack: można jeszcze ze wzorów red. skorzystać, ale jest ok.

TOmek: czyli jak? sin(180−90−α+β)=sin(90−α+β) tak?

TOmek: źle .. cos(90−α+β) nie wiem czy dobrze to "zredukowałem"

TOmek: o pomoc

sushi_ gg6397228:

sin α		sin β		sin γ
	=		=		= 2R ( kat alfa lezy naprzeciw boku "a", kat beta
a		b		c

naprzeciw boku "b" )

think: TOmek zacznijmy od tego, że kąt naprzeciw boku a to (180^o − α − β)