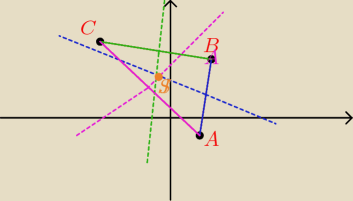
 6.12
A (1; −1) B (3;5) C(−7; 11) znajdź współrzędne środka O okręgu opisanego na tym tójkącie
ja sobie jako O oznaczyłam punkt S, bo zawsze tak robię, że środek czegoś to dla mnie punkt S.
Musimy znaleźć S. Jest pewna własność dot. okręgu opisanego na dowolnych trójkącie, mianowicie
taka, iż symetralne boków trójkąta przecinają się w jednym punkcie − punkcie S, który jest
jednoczeście środkiem okręgu opisanego na tym trójkącie. Czyli żeby znaleźć S musimy znać
równania tych trzech symetralnych (właściwie już dwie symetralne pozwolą nam wyznaczyć ten
punkt) wrzucić je razem w układ równać i wyliczyć x oraz y czyli współrzędne punktu S.
Liczymy najpierw prostą AB, potem jej symetralną ( jest ona prostopadła do prostej AB.
Mając dwa Punkty A i B wyliczamy równanie prostej przechodzącej przez te dwa punkty ze znanego
nam wzoru:
y − yA = { (yB−yA) / (xB−xA) } (x − xA)
y − − 1 = { (5 − − 1) / ( 3 − 1) } (x − 1)
y + 1 = (6/2) * (x−1)
y + 1 = 3x − 3
y = 3x − 4 to jest równanie prostej AB
szukamy środka odcinka AB, aby potem móc użyć wzoru na równanie prostej mając punkt oraz
współczynnik kierunkowy:
A' = { (1+3) / 2 ; (−1 + 5) / 2 }
A' = ( 2; 2)
szukamy prostej prostopadłej do prostej AB (będzie ona jednocześnie symetralną boku AB:
a1 * a2 = −1 gdzie a1 to współczynnik prostej AB, a a2 współ. szukanej prostej prostopadłej
3 * a2 = −1
a2 = − 1/3
mając środek odcinka AB − punkt A' oraz współczynnik kierunkowy a = 1/3 podajemy wzór ja
symetralną boku AB
y − 2 = −1/3 ( x − 2)
y − 2 = −1/3x + 2/3
y = −1/3 x 2 i 2/3
mamy wzór na prostą prostopadłą do prostej AB.
teraz analogicznie robimy z dowolną prostą np AC bądź BC, wyliczamy prostą przechodzącą przez
dwa punkty, liczymy środek danego odcinka, potem wyznaczamy współczynnik kierunkowy i
wyznaczamy wzór na prostą przechodzącą przez jeden punkt i mając dany współcznnim
kierunkowy.
Mając już dwie symetralne, np y1 i y2 wrzucamy je do zwyklego ukladu równań i szukamy x oraz y
− naszych współrzędnych punktu S.
6.12
A (1; −1) B (3;5) C(−7; 11) znajdź współrzędne środka O okręgu opisanego na tym tójkącie
ja sobie jako O oznaczyłam punkt S, bo zawsze tak robię, że środek czegoś to dla mnie punkt S.
Musimy znaleźć S. Jest pewna własność dot. okręgu opisanego na dowolnych trójkącie, mianowicie
taka, iż symetralne boków trójkąta przecinają się w jednym punkcie − punkcie S, który jest
jednoczeście środkiem okręgu opisanego na tym trójkącie. Czyli żeby znaleźć S musimy znać
równania tych trzech symetralnych (właściwie już dwie symetralne pozwolą nam wyznaczyć ten
punkt) wrzucić je razem w układ równać i wyliczyć x oraz y czyli współrzędne punktu S.
Liczymy najpierw prostą AB, potem jej symetralną ( jest ona prostopadła do prostej AB.
Mając dwa Punkty A i B wyliczamy równanie prostej przechodzącej przez te dwa punkty ze znanego
nam wzoru:
y − yA = { (yB−yA) / (xB−xA) } (x − xA)
y − − 1 = { (5 − − 1) / ( 3 − 1) } (x − 1)
y + 1 = (6/2) * (x−1)
y + 1 = 3x − 3
y = 3x − 4 to jest równanie prostej AB
szukamy środka odcinka AB, aby potem móc użyć wzoru na równanie prostej mając punkt oraz
współczynnik kierunkowy:
A' = { (1+3) / 2 ; (−1 + 5) / 2 }
A' = ( 2; 2)
szukamy prostej prostopadłej do prostej AB (będzie ona jednocześnie symetralną boku AB:
a1 * a2 = −1 gdzie a1 to współczynnik prostej AB, a a2 współ. szukanej prostej prostopadłej
3 * a2 = −1
a2 = − 1/3
mając środek odcinka AB − punkt A' oraz współczynnik kierunkowy a = 1/3 podajemy wzór ja
symetralną boku AB
y − 2 = −1/3 ( x − 2)
y − 2 = −1/3x + 2/3
y = −1/3 x 2 i 2/3
mamy wzór na prostą prostopadłą do prostej AB.
teraz analogicznie robimy z dowolną prostą np AC bądź BC, wyliczamy prostą przechodzącą przez
dwa punkty, liczymy środek danego odcinka, potem wyznaczamy współczynnik kierunkowy i
wyznaczamy wzór na prostą przechodzącą przez jeden punkt i mając dany współcznnim
kierunkowy.
Mając już dwie symetralne, np y1 i y2 wrzucamy je do zwyklego ukladu równań i szukamy x oraz y
− naszych współrzędnych punktu S.
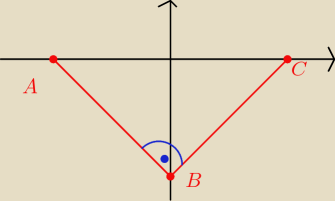 6.14
wykazuje że trójkąt jest prostokątny. widac to z rysunku, ale trzeb wykazać
najłatwiej wykazać że prosta AB jest prostopadła do prostej BC i wtedy bedziemy mieli
rozwiązane zadanie. Mamy podane punkty A (−4; 0) B(0;−4) C(4;0)
równanie prostej AB − z dwóch punktów współnych − znowu stosujemy ten wzór do rybak źle podała
6.14
wykazuje że trójkąt jest prostokątny. widac to z rysunku, ale trzeb wykazać
najłatwiej wykazać że prosta AB jest prostopadła do prostej BC i wtedy bedziemy mieli
rozwiązane zadanie. Mamy podane punkty A (−4; 0) B(0;−4) C(4;0)
równanie prostej AB − z dwóch punktów współnych − znowu stosujemy ten wzór do rybak źle podała
| −4 − 0 | ||
y − 0 = | * (x − −4) | |
| 0 − −4 |
| −4 − 0 | ||
y − −4 = | * (x − 0) | |
| 4 − 0 |