

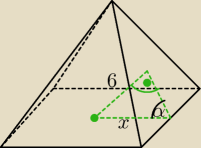
 Tam w ostrosłupie utworzył się trójkąt, gdzie α=60
Więc 6 cm, to wysokośc małego trójkącika, przeciwprostokątna x, to połowa krawędzi podstawy.
Więc najpierw liczymy x:
Tam w ostrosłupie utworzył się trójkąt, gdzie α=60
Więc 6 cm, to wysokośc małego trójkącika, przeciwprostokątna x, to połowa krawędzi podstawy.
Więc najpierw liczymy x:
| 6 | ||
sinα= | ||
| x |
| √3 | 6 | ||
= | |||
| 2 | x |

 zaczynamy to rozgryzać:
masz podane że w podstawie jest kwadrat.
i kąt α=60 stopni
zaczynamy to rozgryzać:
masz podane że w podstawie jest kwadrat.
i kąt α=60 stopni
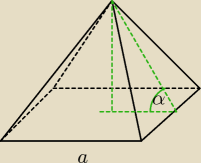 Teraz tam w środku powstał nam trojkąt, którego podstawą jest połową boku podstawy całego
ostrosłupa,
Liczymy więc wysokośc całego ostrosłupa:
Teraz tam w środku powstał nam trojkąt, którego podstawą jest połową boku podstawy całego
ostrosłupa,
Liczymy więc wysokośc całego ostrosłupa:
| H | ||
tgα= | ||
| 4√3 |
| H | ||
√3= | ||
| 4√3 |
| 4√3 | ||
cosα= | ||
| h |
| 1 | 4√3 | ||
= | |||
| 2 | h |

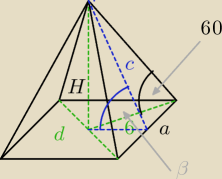 H6 = tg 60° = √3
H = 6√3 a2 +a2 = d2 ⇒a=6√2
V = a2*H*13 ⇒ V = 144√3
c = √(a2)2+H2
pole pow bocz = a*c*2
H6 = tg 60° = √3
H = 6√3 a2 +a2 = d2 ⇒a=6√2
V = a2*H*13 ⇒ V = 144√3
c = √(a2)2+H2
pole pow bocz = a*c*2
| H | ||
tg β = | ||
| a2 |
 Uwzględniłem odległośc od ściany bocznej, a nie krawędzi
Uwzględniłem odległośc od ściany bocznej, a nie krawędzi  U Ciebie dero, ta odległość gdzie jest zaznaczona
U Ciebie dero, ta odległość gdzie jest zaznaczona Bo nie może być wzdłuż płaszczyzny podstawy
Odległość musi być pod kątem prostym
Bo nie może być wzdłuż płaszczyzny podstawy
Odległość musi być pod kątem prostym
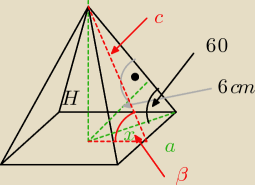 sin 60= 6x =√32 x= 4√3
a = x√2 a = 4√6
H = x√3 = 12
c =√H2+(a2)2 c = 2√42
V = 13a2H
Pb = 2ac
tg β = 2Ha
sin 60= 6x =√32 x= 4√3
a = x√2 a = 4√6
H = x√3 = 12
c =√H2+(a2)2 c = 2√42
V = 13a2H
Pb = 2ac
tg β = 2Ha
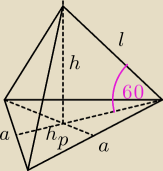 a = 6
a = 6
| a√3 | ||
hp = | = 3√3 | |
| 2 |
| h | |||||||
= tg 60o = √3 | |||||||
|
| 2 | ||
h = | hp*√3 = 2√3*√3 = 6 | |
| 3 |
| a2√3 | ||
Pp = | = 9√3 | |
| 4 |
| Pp*h | 9√3*6 | |||
V = | = | = 18√3 | ||
| 3 | 3 |