Oblicz kąt CMD Milka: w rónwoległoboku ABCD długość boku AB jest 2 razy większa od długości boku BC. Punkt M dzielący bok na AB na połowy połączono z punktami C i D. Obl. kąt CMD

sushi_ gg6397228: rysunek zrobilas co mozna powiedziec o trojkatach MAD i MBC

Milka: tak, rysunek zrobiłam i te trójkąty są równoramienne, czyli kąty w tych trójkątach przy podstawie są równe.

Milka: tera tak się zastanawiam równoramienne czy równoboczne

sushi_ gg6397228: masz trojkaty rownoramienne, tylko katy w wierzcholkach sa rozne (jeden ostry, drugi rozwarty) oznacz kat DAM − α kat CBM− (180−α) policz dla trojkata DAM kat AMD −−> na podstawie "α" policz dla trojkata CBM kat BMC −−> na podstawie "180−α"

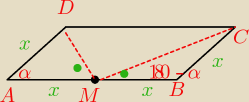
sushi_ gg6397228: policz te katy zaznaczone na zielono

Milka: Piękny rysunek Czyli kąty AMD i ADM są takie same więc można nazwać je β −−−→ α+2β=180 suma kątów w trójkącie DAM, czy należy pójść w kierunku tych boków X − tak? pomocy

sushi_ gg6397228:

	180−α
kat AMD=
	2

	180−(180−α)
kat BMC=
	2

teraz miara kata DMC= 180 − kat AMD − kat BMC

Milka:

	180−α		180−(180−α)
wstawiając do tego obl kąt DMC= 180− (		)−(		wychodzi 90
	2		2

czyli kąt DMC ma 90 stopni

sushi_ gg6397228: to aż zajeło Tobie policzenie tego 5 GODZIN przyłóż ekierke do mojego rysunku, ile tam masz stopni

Milka: wiesz, miałam małe wyjście i dopiero po powrocie wpisałam rozwiązanie. Wielkie dzięki za pomoc jesteś super, ale męczyć jeszcze będę