Wielomiany Jarek: Dlaczego w odpowiedziach pisze że ta nierówność nie ma rozwiązań? 1 − 4x < −4x²

Jack: 4x²−4x+1<0 (2x+1)²<0 Teraz widzisz czemu?

think: ponieważ 4x² − 4x + 1 <0 (2x − 1)² < 0 a to przecież nieprawda bo cokolwiek podniesione do kwadratu nie da liczby mniejszej od 0, oczywiście jeśli mówimy o liczbach rzeczywistych.

Jack: no tak... minus w nawiasie (który i tak nic nie zmienia)...

Basia: 4x²−4x+1<0 Δ=(−4)²−4*4*1=16−16=0

	−b		4		1
x0=		=		=
	2a		8		2

narysuj parabolę, która jest wykresem y=4x²−4x+1 czy jakaś jej część jest pod osią OX ? jeżeli dobrze narysowałeś widzisz, że nie, czyli funkcja nie przyjmuje wartości ujemnych czyli 4x²−4x+1 nigdy nie jest <0

Jarek: Kurde a jak liczyłem z delty wyszło zupełnie co innego

Basia: no to chyba źle tę Δ liczyłeś, bo mnie przy pomocy Δ wyszło to samo co think bez Δ

Jarek: a gdyby było większe lub równe to rozwiązaniem była by liczba ¹₂?

Jarek: no właśnie Basia narysowałem parabole i z niej wchodzi (−nieskończoności ; ¹₂)

Basia: gdyby było =0 to rozwiązaniem byłoby x₀=¹₂ gdyby było >0 to rozwiązaniem byłby R\{¹₂} gdyby było ≥0 to rozwiązaniem byłby cały zbiór R

Jarek: No z nierówności łatwo to odczytać a z paraboli chyba się nie da

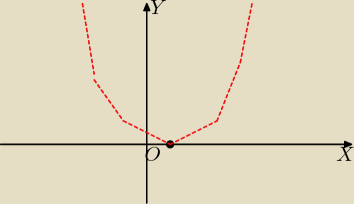
Basia: a to jakim cudem ? przecież ta parabola ma jedno miejsce zerowe i ramiona skierowane do góry gdzie tu jest coś pod osią OX ? o wartości Cię pytają czyli o y

Jarek: a nie przecina?

Jarek: omg tam jest kwadrat więc odbija ehhh sory za kłopot