funkcja kwadratowa Michau: Dla jakich wartości parametru m, równanie: |x²−9|+|x²−16|=m ma dokładnie dwa różne pierwiastki. Ogólnie rozpatrzyłem równanie dla 3 róznych przypadków i dla x∊(−4;−3>∪<3;4) wyszło mi że równanie nie ma pierwiastków, więc rozwiązaniem byłoby m∊∅ , tylko właśnie nie wiem czy dobrze to zrobiłem, więc proszę o pomoc.

Godzio: Jeśli dobrze rozpatrywałeś każdy przypadek to narysuj wykres tego co otrzymałeś i wtedy określ liczbę rozwiązań, jeśli nie będziesz wiedział jak to napisz co Ci wyszło w każdym przypadku to Ci to rozrysuję

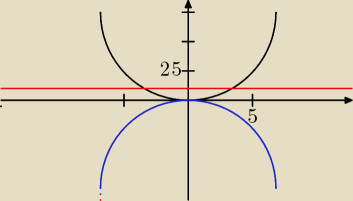
Michau: tak mi wyszło jakoś dziwnie

mac: Mi wychodzi wynik x∊(25,+∞)

Godzio: Dobra rozpiszę Ci to, bo widzę że chyba nie wiesz o co chodzi

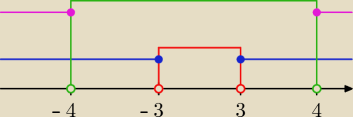
Godzio: |x² − 9| + |x² − 16| = m x² − 9 < 0 ⇒ x ∊ (−3,3) ⇒ |x² − 9| = −x² + 9 x² − 9 ≥ 0 ⇒ x ∊ (∞,−3>∪<3,∞) ⇒ |x² − 9| = x² − 9 x² − 16 < 0 ⇒ x ∊ (−4,4) ⇒ |x² − 16| = −x² + 16 x² − 16 ≥ 0 ⇒ x ∊ (∞,−4>∪<4,∞) ⇒ |x² − 16| = x² − 16 1^o x ∊ (∞,−4>∪<4,∞) f(x) = x² − 9 + x² − 16 = 2x² − 25 2^o x ∊ (−4,−3> ∪ <3,4) f(x) = x² − 9 − x² + 16 = 7 3^o x∊ (−3,3) f(x) = −x² + 9 − x² + 16 = −2x² + 25

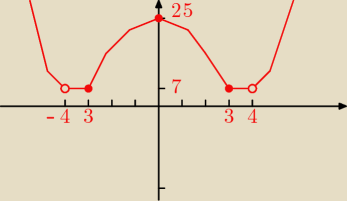
Godzio: Tak wygląda w przybliżeniu ten wykres, jednostki dopasowałem bo miejsca by nie było na tyle I teraz w zależności od prostych m które przecinają wykres mamy: m ∊ (−∞,7) −− brak rozwiązań m ∊ (0,25) −− 4 rozwiązania m = 25 −− 3 rozwiązania m ∊ (25, ∞) −− 2 rozwiązania m = 7 −− nieskończenie wiele rozwiązań

Michau: Ahmm to już mniej więcej rozumiem jak to działa. Dzięki wielkie.