| 4 | ||
Dana jest funkcja f określona wzorem f(x)= | rozwiąż nierówność f(x−1)≥f(x)+1 | |
| x |
| 4 | ||
f(x−1) = | ||
| x−1 |
| 4 | 4 | ||
≥ | +1 | ||
| x−1 | x |
| 4 | 4 | ||
− | −1≥0 | ||
| x−1 | x |
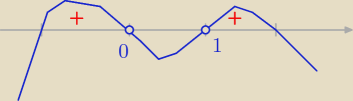 D = R − {0}
D = R − {0}
| 4 | ||
f(x) = | ||
| x |
| 4 | 4 | 4 + x | |||
≥ | + 1 = | x ≠ 0 i x ≠ 1 | |||
| x − 1 | x | x |
| 4 | 4 + x | ||
− | ≥ 0 | ||
| x − 1 | x |
| 4x − (4 + x)(x − 1) | |
≥ 0 | |
| (x − 1)x |
| 1 + √17 | 1 − √17 | |||
x = | v x = | v x = 1 v x = 0 | ||
| 2 | 2 |
| 1 − √17 | 1 + √17 | |||
x ∊ < | , 0) ∪(1, | > | ||
| 2 | 2 |