Kombinatoryka zuzanka:): Ile jest takich rozmieszczeń 10 par skarpetek w 3 szufladach, aby dokładnie 1 był pusta.

Jack: 3 (2¹⁰−2)

zuzanka:): nie rozumie mógłbyś to jakoś wytłumaczyć Bardzo proszę .

Basia: coś się nie zgadza Jack 10→2 czyli 2¹⁰ i odrzucam przypadki, że jedna z tych dwóch pusta 2¹⁰−2 razem 3(2¹⁰−2) Twój wynik −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− wybieram jedną z trzech 3*2¹⁰ odrzucam przypadki gdy dwie puste czyli (1,2) (1,3) (2,3) 3*2¹⁰−3 = 3*(2¹⁰−1) gdzie tkwi błąd ?

Jack: wybieramy szufladę, która będzie pusta, na 3 sposoby. Zostają więc dwie szuflady (Sz₁ i Sz₂) do których pakuję skarpetki. Pierwsza skarpetka ma 2 opcję, druga ma dwie opcje itd aż do dziesiątej, która tez ma dwie opcję. Robimy więc wariację z powtórzeniami i wychodzi 2¹⁰. Jednak wśród wszystkich takich możliwości są dwie, które nam nie pasują: że wszystkie skarpetki wrzucimy do Sz₁ lub że wszystkie wpadną do Sz₂ (wtedy aż dwie szuflady byłyby puste). Dlatego od wszystkich opcji których jest 2¹⁰ należy odjąć te 2 sytuacje i ogólnie wyjdzie 3 * (2¹⁰−2)

Basia: rozumiem Twoje rozumowanie i wydaje mi się poprawne, ale przeanalizuj moje też wydaje mi się poprawne, a wyniki różne dlaczego ?

Jack: 3*2¹⁰ − co w ten sposób liczysz? Wg mnie to, że co najmniej jedna będzie pusta. Jeśli tak, to zeby odrzucić przypadki że więcej niz jedna będzie pusta, nie wystarczy odjąć 3 przypadków ale 3*2 − czyli trzeba uzależnić to jeszcze od początkowego wyboru pierwotnej pustej szufladki.

zuzanka:): a wynik nauczyciel nam podał 45 * 2⁸

Basia: masz rację, to mnie przekonało ale dlaczego wynik ma być 45*2⁸ nie pojmuję (i chyba nie pojmę)

zuzanka:): dokładnie siedzę nad tym już 3 dzień i nie wiem

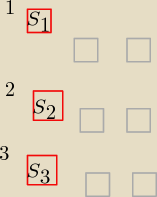
Jack: Czerwone to wybór pierwotny, szare do dwa przypadki gdy któraś z pozostałych szuflad jest pusta. Widać teraz, że wychodzi 2*3 przypadków. (mam nadzieję ze sensownie to zobrazowałem)

Basia: musi być tak jak napisał Jack 3*(2¹⁰−2)=6(2⁹−1)

Jack: oo... nie odświeżyłem strony.

zuzanka:): ok. dzięki

Jack: no tak, tajemnicza ta odpowiedź

Basia: Jack, ale tam się niektóre przypadki pustych będą pokrywały (s₁, s₂) puste ⇔ wszystko w s₃ (s₁,s₃) puste ⇔ wszystko w s₂ (s₂,s₁) puste ⇔ wszystko w s₃ (s₂,s₃) puste ⇔ wszystko w s₁ (s₃,s₁) puste ⇔ wszystko w s₂ (s₃,s₂) puste ⇔ wszystko w s₁ Ty je liczysz wszystkie, a naprawdę jest ich tylko 3

zuzanka:): Ja myslałam żeby to zrobić tak wariacja z powtorzeniami 2¹0* 3 *6 poniewaz szuflady tez mogą się przemieszczać

zuzanka:): Ja myslałam żeby to zrobić tak wariacja z powtorzeniami 2¹⁰* 3 *6 poniewaz szuflady tez mogą się przemieszczać

Jack: Wdaje mi się, Basiu, że przy takim liczeniu: 3*2¹⁰ (i tym moim też), jest to usprawiedliwione. Ja po prostu zliczam dla każdej wybranej pierwotnie pustej szuflady takie sytuacje, które mi odpowiadają. Może się zdarzyć że odejmę dwa razy jakiś element (przy różnych pierwotnych szufladach (!) ), ale to dlatego, że ze sposobu zliczania, jaki przyjąłem, wynika, że dopuszczam takie powtórzenia.

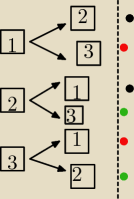
Basia: kropki jednego koloru pokazują jeden in ten sam przypadek, który Ty liczysz podwójnie

Basia: będę się wobec tego upierać, że = 3*2¹⁰−3 = 3*(2¹⁰−1) kilka lat temu było już to zadanie, pamiętam dyskusję też taką samą w końcu stanęliśmy na tym wyniku, ale .....

Jack: każda pierwotnie wybrana szuflada generuje pewne przypadki, które należy odrzucić. Wydaje mi się, że nic nie stoi na przeszkodzie, aby dwie szuflady generowały taką samą sytuację nie do przyjęcia. Dlatego należy je obie odrzucić. Ale wszystko to jest wynikiem przyjętej metody zliczania.

Jack: ja pamiętam, że kiedyś na zajęciach z RP też miałem takie zadanie i prowadzący przyjął za dobre rozwiązanie to polegające na odjęciu dwóch przypadków. Nie jest to żaden specjalny wyznacznik, ale wydaje mi się to rozwiązanie sensowne.

Basia: 3 litery 3 szuflady 1pusta,2ab,3c 1pusta,2ac,3b 1pusta,2bc,3a 1pusta 2a,3bc 1pusta,2b,3ac 1pusta,2c,3ab 6 możliwości, innych nie ma to samo dla 2 pustej i 3 pustej razem 3*6=18 liczymy teraz bez wypisywania 3*(2³−2) = 3*8−6=24−6=18 masz rację i wiem gdzie popełniłam błąd, ale już nie chce mi się tego opisywać −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− zuzanka ma być tak jak podał Jack 3*(2¹⁰−2)=6(2⁹−1)

Jack: cieszę się, że (jak się wydaje) rozwialiśmy swoje wątpliwości. Też miałem rozpisać przykład dla 3 szufladek i 3 skarpetek, na którym widać, że odjęcie dokładnie dwóch przypadków jest niezbędne.

Basia: błąd polegał na tym, że nie przyjęłam do wiadomości, że pisząc 3*2¹⁰ też podwójnie liczę przypadki, w których dwie są puste