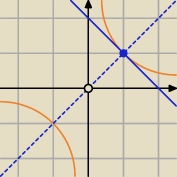
Jak wyznaczyć wzór tej funkcji? Bohdan: Wyznacz równanie prostej y=ax+b (a≠0), której jedynym punktem wspólnym z wykresem funkcji y=¹_x jest punkt (1,1). Oblicz pole trójkąta ograniczonego osiami współrzędnych i tą prostą.

Grześ: Aby miała tylko jeden punkt wspólny musi być prostą pionową lub poziomą, skoro jest wyrzucony warunek prostej poziomej, zostaje pionowa: gdzie a=1, b=0, y∊R x=1

ostr: A gdyby tak wyznaczyć równanie stycznej do krzywej y=¹_x w punkcie (1,1) ?

Godzio: 1 = a + b b = 1 − a y = ax + 1 − a

1
	= ax + 1 − a
x

1 = ax² + x − ax ax² + x(1 − a) − 1 = 0 a ≠ 0 Δ = 0 (bo jeden punkt wspólny ) Δ = 1 − 2a + a² + 4a = a² + 2a + 1 = (a + 1)² = 0 ⇒ a = −1 Odp: y = −x + 2 Z trójkątem sobie chyba poradzisz

ostr: Godzio, fajnie to policzyłeś Ja znalazłem pochodną 1/x i dopiero dalej ze wzoru styczną.

Godzio: Tak też można było, tyle że to raczej LO a nie studia tak myślę...

Bogdan: 1 = a*1 + b ⇒ a = 1 − b

	1
Prosta y = ax + b mająca jeden punkt wspólny z hiperbolą y =		jest styczną tej
	x

hiperboli.

1
	= ax + b ⇒ ax2 + bx − 1 = 0, x ≠ 0.
x

Δ = 0 ⇒ b² + 4a = 0 ⇒ b² + 4 − 4b = 0 ⇒ (b − 2)² = 0 ⇒ b = 2 i a = 1 − 2 = −1 Odp.: y = −x + 2 Pole trójkąta jest łatwe do wyznaczenia.

Bohdan: Kurcze, takie to proste, chyba mi dziś mózg odparował Dzięki wielkie