przekątne rombu Sevento: Bok rombu ma długość 5cm a jeden z jego katów ma miare 54 stopni. Jakie długości mają przekątne tego rombu? Proszę o rozwiązanie zadania.

Gustlik: Najpierw oblicz pole rombu ze wzoru: P=a²sinα=25*sin54^o≈20,23 Oznacz sobie przekątne e=2x, f=2y Wzór na pole rombu z przekątnych:

	1
P=		ef
	2

Zatem

	1
P=		*2x*2y=2xy
	2

Masz układ równań: { 2xy=20,23 { x²+y²=25 (tw. Pitagorasa − przekatne przecinają się w rombie pod kątem prostym, czyli połówki przekątnych i bok rombu tworzą trójkąt prostokątny) Rozwiąż ten układ równań − wskazówka: dodaj stronami równania, po lewej stronie otrzymasz wzór skróconego mnozenia.

Olek: a może tak: p=10sin27^o p=10cos27^o

Basia: ja bym zastosowała tw.sinusów

e		a
	=
sin54		sin63

	a*sin54		a*sin(2*27)
e =		=		=
	sin63		sin(90−27)

2a*sin27*cos27
	=2a*sin27 = 10*sin27
cos27

f		a
	=
sin126		sin27

f		a
	=
sin54		sin27

	a*sin54		a*2sin27*cos27
f =		=		=2a*cos27=10*cos27
	sin27		sin27

Basia: i nie tylko ja, Olek chyba też

Bogdan:

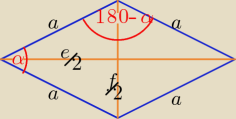
e     2		α		α
	= cos		⇒ e = 2acos
a		2		2

f     2		α		α
	= sin		⇒ f = 2asin
a		2		2

Basia: no a Bogdan porządnie narysował i od razu wszystko proste i jasne

Sevento: { 2xy=20,23 { x2+y2=25 Może ktoś rozwiązać? Bo ja się boję, że mi źle wyjdzie i wpiszę złą odpowiedź...