geometria analityczna klaudia0905: Znaleźć kąt między przekątnymi równoległoboku zbudowanego n wektorach a^→=[6,1,−3] b^→=[−2,2,4]

AS: Poszukaj podstawowego wzoru albo wyprowadź,podstaw dane i po strachu.

klaudia0905: tylko, że po pierwsze w równoległoboku kiedy przetną się przekątne to są dwa różne kąty, a po drugie trzeba tu obliczyć dł. obu przekątnych i punkt przecięcia a niestety nie wiem jak.

Basia: c,d przekatne c^→=a^→+b^→ d^→=−a^→+b^→ oblicz współrzędne c^→, d^→, |c|, |d| i iloczyn skalarny z wzoru c^→od^→=c₁*d₁+c₂*d₂+c₃*d₃ i porównaj z definicją c^→od^→==|c|*|d|*cos∡(c^→,d^→) z tego wyliczysz cos∡(c^→,d^→) a więc także i kąt α; drugi = 180−α

Basia: punktu przecięcia w tym zadaniu na pewno nie da się znaleźć

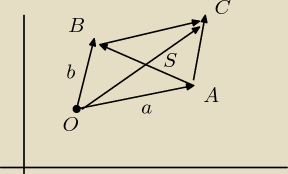
AS: Przyjmuję dowolny punkt zaczepienia np. O(1,1,1) Wyznaczam współrzędne punktów A i B dla punktu A dla punktu B xA = 1 + ax = 1 + 6 = 7 xB = 1 + bx = 1 + (−2) = −1 yA = 1 + ay = 1 + 1 = 2 yB = 1 + by = 1 + 2 = 3 zA = 1 + az = 1 + (−3) = −2 zb = 1 + 4 = 5 Współrzędne A (7,2,−2) B(−1,3,5) Wyznaczam wsp.punktu C

	xA + XB		7 − 1
xS =		=		= 3
	2		2

analogicznie yS = 5/2 , zS = 3/2

	xO + xC		1 + xC
xS =		⇒ 3 =		⇒ xC = 5
	2		2

analogicznie yS = 4 , zS = 2 S(5,4,2) Wsp. wektora OC = [4,3,1] , wektora AB = [−8,1,7] Długość wektora OC = √4² + 3² + 1² = √26 Długość wektora AB = √(−8)² + 1² + 7² = √114 cos kąta między nimi

	|4*(−8) + 3*1 + 1*7|		22
cosα =		=
	√26*√114		√26*√114